题目内容
为解方程(x2-1)2-5(x2-1)+4=0,我们可以将x2-1视为一个整体,然后设x2-1=y,则y2=(x2-1)2,原方程化为y2-5y+4=0,解此方程,得y1=1,y2=4。当y=1时,x2-1=1,x2=2,∴x=±![]() 。
。
当y=4时,x2-1=4,x2=5,∴x=±![]() 。
。
∴原方程的解为x1=-![]() ,x2=
,x2=![]() ,x3=-
,x3=-![]() ,x4=
,x4=![]() 。
。
以上方法就叫换元法,达到了降次的目的,体现了转化的思想。
(1)运用上述方法解方程:x4-3x2-4=0。
(2)既然可以将x2-1看作一个整体,你能直接运用因式分解法解这个方程吗?
答案:
解析:
解析:
| 解:(1)设x2=y,则原方程化为y2-3y-4=0,解得y=4或-1(舍去)
∴x2=4 ∴x1=-2,x2=2 (2) (x2-2)(x2-5)=0 (x+
|

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
 ,∴x=±,
,∴x=±, 做换元法;
做换元法; ;当y=4时,x2-1=4,
;当y=4时,x2-1=4,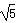 ,
,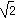 ;当y=4时,x2-1=4,
;当y=4时,x2-1=4,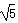 ,
,