福建省厦门第一中学2008―2009学年度
第一学期期中考试
高二年文科数学试卷
命题教师:廖献武 审核教师:郭仲飞 2008.11
A卷(共100分)
一、选择题:(共12题,每题5分,共60分)
1.算法的三种基本逻辑结构是( )
A.顺序结构、模块结构、条件结构 B.顺序结构、条件结构、循环结构
C.顺序结构、循环结构、模块结构 D.模块结构、条件结构、循环结构
2.将51化为二进制数得( )
A.A.100111(2) B.110110(2) C. 110101(2) D. 110011(2)
3.下列命题不正确的是( )
A.使用抽签法,每个个体被抽中的机会相等;
B.使用系统抽样从容量为N的总体中抽取容量为n的样本,确定分段间隔k时,若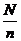 不是整数,则需随机地从总体中剔除几个个体;
不是整数,则需随机地从总体中剔除几个个体;
C.分层抽样就是随意的将总体分成几部分;
D.无论采取怎样的抽样方法,必须尽可能保证样本的代表性.
4. 等差数列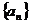 中
中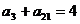 ,则前
,则前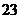 项的和
项的和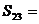 ( )
( )
A.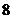 B.
B.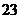 C.
C.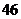 D.
D.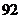
5.在抽查某产品尺寸的过程中,将其尺寸分成若干组,[a,b]是其中一组,抽查出的个数在该组上的频率为m,该组上的直方图的高为h,则 ?a-b?等于 ( )
A.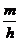 B.
B.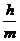 C.hm D.与m,h无关
C.hm D.与m,h无关
6.如果命题“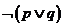 ”为假命题,则
( )
”为假命题,则
( )
A.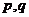 均为真命题 B.
均为真命题 B.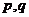 中至少有一个是真命题
中至少有一个是真命题
C.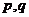 均为假命题 D.
均为假命题 D.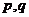 中至多有一个是真命题
中至多有一个是真命题
7.从装有两个红球和两个黑球的口袋里任取两个球,那么互斥而不对立的两个事件是( )
A.“至少有一个黑球”与“都是黑球” B.“至少有一个黑球”与“至少有一个红球”
C.“至少有一个黑球”与“都是红球” D.“恰好有一个黑球”与“恰好有两个黑球”
8. 条件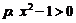 ,条件
,条件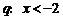 ,则
,则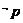 是
是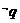 的
( )
的
( )
A.充分但不必要条件 B.必要但不充分条件
C.充分且必要条件 D.既不充分也不必要条件
9.执行右边的程序框图,若p=0.8,则输出的n= ( )
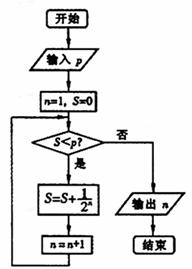 A. 1 B.
A. 1 B.
10.甲、乙、丙三人随意入住三间空房,则甲、乙、丙三人各住一间房的概率是 ( )
A.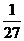 B.
B.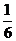 C.
C. 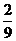 D.
D.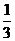
11.函数f(x)=x2-x-2 x∈[
-5,5 ],那么任取一点x0∈[ -5,5
],使f(x0)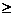 0的概率是 ( )
0的概率是 ( )
A.1 B.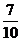 C.
C.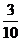 D.
D.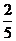
12.盒中有10只螺丝钉,其中有3只是坏的,现从中随机地抽取4个,那么 等于 ( )
等于 ( )
A.恰有1只是坏的的概率 B.4只全是好的的概率
C.恰有2只是好的的概率 D.至多1只是坏的的概率
二、填空题:(共2题,每题4分,共8分)
13.命题P: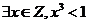 .则
.则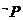 为
.
为
.
14.函数 的单调增区间为
.
的单调增区间为
.
三、解答题:(共3题,15题10分、16题10分、17题12分,共32分)
15.甲、乙两人在相同的条件下的射击测试中各射靶10次,各次命中的环数如下:
甲 7 8 7 9 5 4 9 10 7 4
乙 4 7 8 6 8 6 5 9 10 7
(1)分别计算甲、乙命中环数的中位数和平均数;
(2)计算上面两个样本的标准差,从计算结果看,谁射击的情况比较稳定.
16.下面是某位同学利用当型循环语句写的一个求满足1+2+3+…+n
> 500的最小的自然数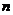 的程序.
的程序.
|
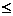 f(x)成立的x的取值范围.
f(x)成立的x的取值范围.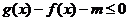 恒成立,求
恒成立,求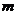 的取值范围.
的取值范围.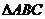 的中心为
的中心为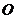 ,则
,则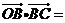 .
.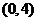 内任取两个数,则这两个数的和不小于2的概率为
.
内任取两个数,则这两个数的和不小于2的概率为
.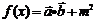 ,其中向量
,其中向量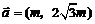 ,
,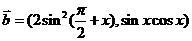 ,
,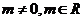 )
)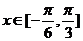 ,f(x)的最大值大于10,求
,f(x)的最大值大于10,求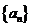 满足
满足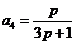 (0<
(0<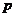 <1,
<1,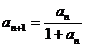 (
(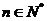 )
) 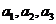 的值;
的值;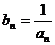 ,求证:数列
,求证:数列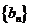 为等差数列,并求
为等差数列,并求 .
.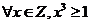 14、
14、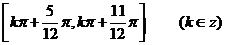
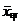 、
、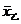
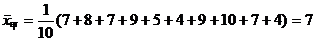 …………………………………………3分
…………………………………………3分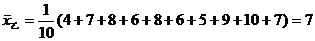 …………………………………………5分
…………………………………………5分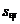 、
、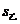
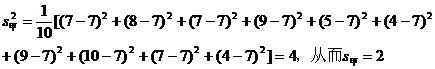
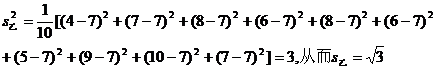 ……………………9分
……………………9分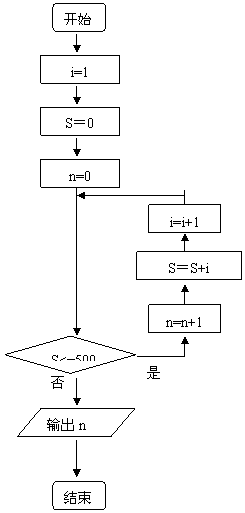 (1) y=g(x)=log2(3x+1) ………………3分
(1) y=g(x)=log2(3x+1) ………………3分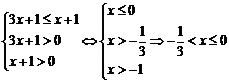
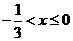 .………7分
.………7分 恒成立, ∴
恒成立, ∴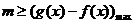 ……9分
……9分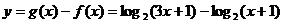
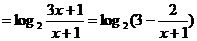
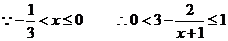 ,
,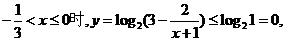
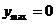 , ∴
, ∴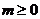 .……………12分
.……………12分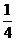 ; 19、
; 19、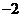 ; 20、
; 20、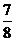 ; 21、
; 21、 .
. 种不同的抽法.
………………………………2分
种不同的抽法.
………………………………2分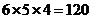 (种)
(种)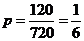 .
…………………………………………6分
.
…………………………………………6分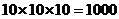 种不同方法.
种不同方法.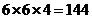 种方法;
种方法;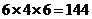 种方法;
种方法;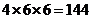 种方法;
种方法;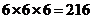 种方法;
种方法;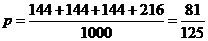 . ………………………………10分
. ………………………………10分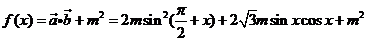 ………………2分
………………2分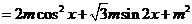
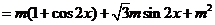 ……4分
……4分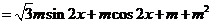
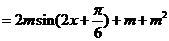 …………5分
…………5分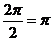 ;
…………………………………………6分
;
…………………………………………6分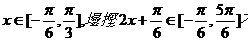
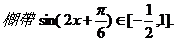 …………9分
…………9分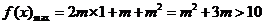 ,解得:m>2(m<-5舍去).
,解得:m>2(m<-5舍去).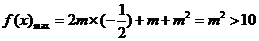 , 解得:
, 解得: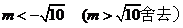 ,
,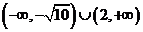 . …………………………………………12分
. …………………………………………12分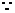
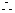
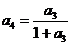 把
把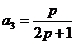 ,
,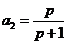 ;
;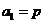 . ………………………………………………………3分
. ………………………………………………………3分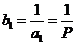
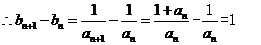
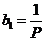 为首项,以1为公差的等差数列 (或由
为首项,以1为公差的等差数列 (或由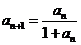 直接推出
直接推出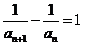 相应给分) ………………………………………………………………7分
相应给分) ………………………………………………………………7分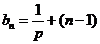 ………………………………………………………………………8分
………………………………………………………………………8分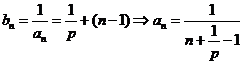 ……………………………………9分
……………………………………9分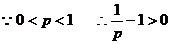
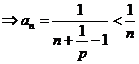 ……………………………………10分
……………………………………10分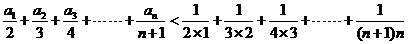
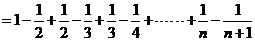
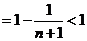 ……………………………………12分
……………………………………12分