摘要：(3)求证:. 高二年文科数学试卷答案A卷 B D C C A B D A D C B D
网址：http://m.1010jiajiao.com/timu_id_207025[举报]
(理)已知数列{an}的前n项和为Sn,且满足a1=
,an+2SnSn-1=0(n≥2),
,an+2SnSn-1=0(n≥2),(1)判断{
}是否为等差数列?并证明你的结论;
(2)求Sn和an;
(3)求证:S12+S22+…+Sn2≤
.
(文)数列{an}的前n项和Sn(n∈N*),点(an,Sn)在直线y=2x-3n上.
(1)求证:数列{an+3}是等比数列;
(2)求数列{an}的通项公式;
(3)数列{an}中是否存在成等差数列的三项?若存在,求出一组适合条件的三项;若不存在,请说明理由.
查看习题详情和答案>>
(理)已知:fn(x)=a1x+a2x2+…+anxn,fn(-1)=(-1)n·n,n=1,2,3,….
(1)求a1、a2、a3;
(2)求数列{an}的通项公式;
(3)求证:fn(
)＜1.
(文)设函数f(x)=2ax3-(6a+3)x2+12x(a∈R),
(1)当a=1时,求函数f(x)的极大值和极小值;
(2)若函数f(x)在区间(-∞,1)上是增函数,求实数a的取值范围.
查看习题详情和答案>>
(理)已知数列{an}的前n项和为Sn,且满足a1=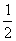
,an+2SnSn-1=0(n≥2),
,an+2SnSn-1=0(n≥2),(1)判断{
}是否为等差数列?并证明你的结论;
(2)求Sn和an;
(3)求证:S12+S22+…+Sn2≤
.
(文)数列{an}的前n项和Sn(n∈N*),点(an,Sn)在直线y=2x-3n上.
(1)求证:数列{an+3}是等比数列;
(2)求数列{an}的通项公式;
(3)数列{an}中是否存在成等差数列的三项?若存在,求出一组适合条件的三项;若不存在,说明理由.
查看习题详情和答案>>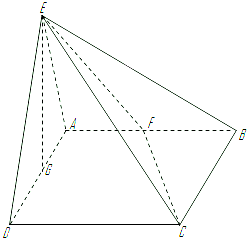
如图，平面EAD⊥平面ABCD，△ADE是等边三角形，ABCD是矩形，F是AB的中点，G是AD的中点，EC与平面ABCD成30°角，（1）（理、文）求证EG⊥平面ABCD；
（2）（理、文）当AD的长是多少时，D点到平面EFC的距离为2？请说明理由．
（3）（理答文不答）若AD=2，求二面角E-FC-G的度数．
对支霄一中高二年段学生是爱好体育还是爱好文娱进行调查，共调查了40人，其中男生25人，女生15人．男生中有15人爱好体育，另外10人爱好文娱．女生中有5人爱好体育，另外10人爱好文娱；
（1）根据以上数据制作一个2×2的列联表；
（2）若要从爱好体育和从爱好文娱的学生中各选一人分别作文体活动的协调人，求选出的两人恰好是一男一女的概率；
（3）在多大的程度上可以认为性别与是否爱好体育有关系？
附：K2=
（此公式也可写成X2=
）
参考数据：
查看习题详情和答案>>
（1）根据以上数据制作一个2×2的列联表；
（2）若要从爱好体育和从爱好文娱的学生中各选一人分别作文体活动的协调人，求选出的两人恰好是一男一女的概率；
（3）在多大的程度上可以认为性别与是否爱好体育有关系？
附：K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| n(n11n22-n12n21)2 |
| n1+n2+n+1n+2 |
参考数据：
| P（K2≥k） | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |