体育考试的成绩的等级为优、良、中、不及格的事件分别记为．在同一次体育考试中，同一人不能同时既得优又得良，即事件是不可能同时发生的．将这种不可能同时发生的事件称互斥事件。

在上述关于体育考试成绩的问题中，用事件表示事件“优”和“良”，那么从50人中任意抽取1个人，有50种等可能的方法，而抽到优良的同学的方法有9+15种，从而事件发生的概率．  另一方面，，因此有．

三、建构数学

1．即事件Ａ 与Ｂ 是不可能同时发生的．不能同时发生的两个事件称为互斥事件。

2．事件Ａ，Ｂ，Ｃ，Ｄ，其中任意两个都是互斥的．一般地，如果事件Ａ_１，Ａ_２，…，Ａ_ｎ中的任何两个都是互斥事件，就说事件Ａ_１，Ａ_２，…，Ａ_ｎ彼此互斥．

3．设Ａ，Ｂ 为互斥事件，当事件Ａ，Ｂ 有一个发生，我们把这个事件记作Ａ＋Ｂ．在上述关于体育考试成绩的问题中，事件Ａ＋Ｂ 就表示事件“优”或“良”，那么，事件Ａ＋Ｂ 发生的概率是多少呢？

由以上分析不难发现，概率必须满足如下第三个基本要求：

如果事件Ａ，Ｂ 互斥，那么事件Ａ＋Ｂ 发生的概率，等于事件Ａ，Ｂ 分别发生的概率的和，即

Ｐ(Ａ＋Ｂ)＝Ｐ(Ａ)＋Ｐ(Ｂ)．

一般地，如果事件Ａ_１，Ａ_２，…，Ａ_ｎ两两互斥，则

Ｐ(Ａ_１＋Ａ_２＋ … ＋Ａ_ｎ)＝Ｐ(Ａ_１)＋Ｐ(Ａ_２)＋ … ＋Ｐ(Ａ_ｎ)．

两个互斥事件必有一个发生，则称这两个事件为对立事件．事件Ａ 的对立事件记为．

图示为：

关系：{x|x为对立事件}{x|x为互斥事件}

对立事件与Ａ必有一个发生，故＋Ａ是必然事件，从而

Ｐ（）＋Ｐ（Ａ）＝Ｐ（＋Ａ）＝１．

由此，我们可以得到一个重要公式：

Ｐ（）＝１－Ｐ（Ａ）．

四、数学运用

1．例题

例1  一只口袋内装有大小一样的４只白球与４只黑球，从中一次任意摸出２只球．记摸出２只白球为事件Ａ，摸出１只白球和１只黑球为事件Ｂ．问：事件Ａ 与Ｂ 是否为互斥事件？是否为对立事件？

解  事件和互斥

因为从中一次可以摸出2只黑球，所以事件和不是对立事件．

练习：果事件A、B互斥，那么               　　　　（     ）

． A+B是必然事件?． +是必然事件．与一定互斥?            ． 与一定不互斥       (B)

例2  某人射击１次，命中７～１０环的概率如表所示：

命中环数

10环

9环

8环

7环

概率

0.12

0.18

0.28

0.32

　（１）求射击１次，至少命中７环的概率；

（２）求射击１次，命中不足７环的概率．

解  记事件“射击1次，命中环”为则事件两两相斥．

（1）记“射击一次，至少命中7环”的事件为，那么当，，或之一发生时，事件发生．由互斥事件的概率加法公式，得
=
=．

（2）事件“射击一次，命中不足7环”是事件“射击一次，命中至少7环”的对立事件，即表示事件“射击一次，命中不足7环”．根据对立事件的概率公式，得

．

答  此人射击1次，至少命中7环的概率为0.9；命中不足7环的概率为0.1．

思考；甲、乙同时向一个目标进行射击，甲击中的概率为0.4,乙击中的概率为0.5,则目标被击中的概率是否为0.4+0.5=0.9?如果不是，说明理由？

（不是，甲、乙击中目标不互斥）

例3  黄种人群中各种血型的人所占的比如表所示：

血型

A

B

AB

O

该血型所占比%

28

29

8

35

已知同种血型的人可以输血，Ｏ 型血可以输给任一种血型的人，任何人的血都可以输给 ＡＢ型血的人，其他不同血型的人不能互相输血．小明是Ｂ型血，若小明因病需要输血，问：（１）任找一个人，其血可以输给小明的概率是多少？

（２）任找一个人，其血不能输给小明的概率是多少？

解  （1）对任一人，其血型为A，B，AB，O型血的事件分别记为它们是互斥的．由已知，有．

因为B，O型血可以输给B型血的人，故“可以输给B型血的人”为事件．根据互斥事件的加法公式，有．

（2）由于A，AB型血不能输给B型血的人，故“不能输给B型血的人”为事件，且．

答  任找一人，其血可以输给小明的概率为0.64，其血不能输给小明的概率为0.36．

注 ：第（2）问也可以这样解：因为事件“其血可以输给B型血的人”与事件“其血不能输给B型血的人”是对立事件，故由对立事件的概率公式，有

五、回顾小结

1．互斥事件和对立事件的概念；

2．互斥事件中有一个发生的概率的计算公式；

3．对立事件的概率间的关系．

六、课外作业：

课本第108页第1~7题．

课题： 3．4  互斥事件（2）

教学目标：

1、知识与技能：

      （1）正确理解事件的包含、并事件、交事件、相等事件，以及互斥事件、对立事件的概念；

（2）概率的几个基本性质：

1）必然事件概率为1，不可能事件概率为0，因此0≤P(A)≤1；

2）当事件A与B互斥时，满足加法公式：P(A+B)= P(A)+ P(B)；

3）若事件A与B为对立事件，则A+B为必然事件，

所以P(A+B)= P(A)+ P(B)=1，于是有P(A)=1―P(B)

（3）正确理解和事件与积事件，以及互斥事件与对立事件的区别与联系.

2、过程与方法：通过事件的关系、运算与集合的关系、运算进行类比学习，培养学生的类化与归纳的数学思想。

3、情感态度与价值观：通过数学活动，了解教学与实际生活的密切联系，感受数学知识应用于现实世界的具体情境，从而激发学习 数学的情趣。

教学重点：概率的加法公式及其应用

教学难点：事件的关系与运算

教学过程：

练习：教材P108---练习题

二、数学运用

例1．盒中有6只灯泡，其中2只次品，4只正品，有放回地从中任取两次，每次取一只，试求下列事件的概率：

(1)取到的2只都是次品；            (2)取到的2只中正品、次品各一只；?

(3)取到的2只中至少有一只正品．?

解：从6只灯泡中有放回地任取两只，共有36种不同取法．?

(1)取到的2只都是次品情况为种．因而所求概率为．?

(2)由于取到的2只中正品、次品各一只有两种可能：第一次取到正品，第二次取到次品；及第一次取到次品，第二次取到正品．因而所求概率为．

(3)由于“取到的两只中至少有一只正品”是事件“取到的两只都是次品”的对立事件．因而所求概率为．

例2． 袋中有12个小球，分别为红球、黑球、黄球、绿球，从中任取一球，得到红球的概率为，得到黑球或黄球的概率是，得到黄球或绿球的概率也是，试求得到黑球、得到黄球、得到绿球的概率各是多少？

解：设得到红球、得到黑球、得到黄球、得到绿球依次为事件A、B、C、D，根据题意得

　解得：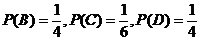

练习：从男女学生共有36名的班级中，任意选出2名委员，任何人都有同样的当选机会．如果选得同性委员的概率等于，求男女生相差几名?

解：设男生有名，则女生有名．选得2名委员都是男性的概率为．

选得2名委员都是女性的概率为?．

上两种选法是互斥的，又选得同性委员的概率等于，

得?．解得或?

即男生有15名，女生有36-15=21名，或男生有21名，女生有36-21=15名．

总之，男女生相差6名．

三、作业：

1．回答下列问题：?

(1)甲、乙两射手同时射击一目标，甲的命中率为0．65，乙的命中率为0．60，那么能否得出结论：目标被命中的概率等于0．65＋0．60＝1．25，为什么?

(2)一射手命中靶的内圈的概率是0．25，命中靶的其余部分的概率是0．50，那么能否得出结论：目标被命中的概率等于0．25＋0．50＝0．75，为什么??

(3)两人各掷一枚硬币，“同时出现正面”的概率可以算得为．由于“不出现正面”是上述事件的对立事件，所以它的概率等于这样做对吗?说明道理．

解: (1)不能．因为甲命中目标与乙命中目标两事件不互斥．?

(2)能．因为命中靶的内圈和命中靶的其余部分是互斥事件．?

(3)不对．因为“不出现正面”与“同时出现正面”不是对立事件，故其概率和不为1．

2． 某市派出甲、乙两支球队参加全省足球冠军赛．甲乙两队夺取冠军的概率分别是 和．试求该市足球队夺得全省足球冠军的概率．()

3． 在房间里有4个人．问至少有两个人的生日是同一个月的概率是多少? ()

5．某单位36人的血型类别是：A型12人，B型10人，AB型8人，O型6人．现从这36人中任选2人，求此2人血型不同的概率．()