2009-2010学年度潍坊市高密初中学段第一学期九年级期中考试
数学试卷
(时间:90分钟 满分120分)
一、选择题:(共12个小题,每小题3分,共36分)请把正确答案的序号填入下表中
1.下列二次根式中属于最简二次根式的是
A.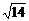
 B.
B.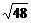 C.
C.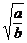 D.
D.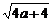
2.若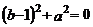 ,则下列方程中是一元二次方程的是
,则下列方程中是一元二次方程的是
A.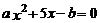 B.
B.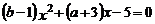
C.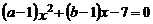 D.
D.
3.以三角形的一条中位线和第三边上的中线为对角线的四边形是
A.梯形 B.平行四边形 C.菱形 D.矩形
4.设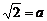 ,
,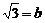 ,用含
,用含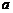 、
、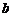 的式子表示
的式子表示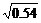 ,则下列表示正确的是
,则下列表示正确的是
A.0.3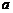
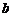 B.
B.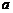
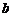 C.0.1
C.0.1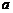
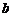 D.0.1
D.0.1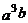
5.小明的作业本上有以下四题:
①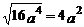 ②
②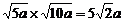
③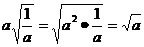 ④
④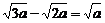
如果你是他的数学老师,请找出他做错的题是
A.① B.② C.③ D.④
6.如图所示,在长为8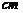 ,宽为6
,宽为6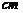 的矩形中,截去一个矩形(图中阴影部分),如果剩下的矩形与原矩形相似,那么剩下矩形的面积是
的矩形中,截去一个矩形(图中阴影部分),如果剩下的矩形与原矩形相似,那么剩下矩形的面积是

A.28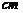 2 B.27
2 B.27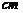 2 C.21
2 C.21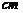 2 D.20
2 D.20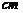 2
2
7.若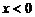 ,则
,则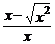 的结果是
的结果是
A.0 B.一2 C.0或―2 D.2
8.已知关于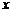 的方程
的方程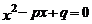 的两个实数根分别是0和-2,则p和q的值分别是
的两个实数根分别是0和-2,则p和q的值分别是
A.p=2 q=0 B.p=-2 q=0 C.p=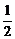 q=0 D.p=
q=0 D.p=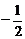 q=0
q=0
9.若一元二次方程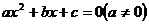 满足
满足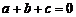 ,且该方程有两个相等的实数根,则下列结论正确的是
,且该方程有两个相等的实数根,则下列结论正确的是
A.a=c B.a=b C.b=c D.a=b=c
10.如图,点D为△ABC的AB边上一点(AB>AC),下列条件不一定能保证△ACD∽△ABC的是
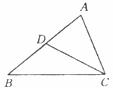
A.∠ADC=∠ACB B.∠ACD=∠B C.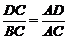 D.
D.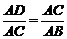
11.设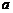 ,
,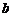 是方程
是方程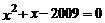 的两个实数根,则
的两个实数根,则 的值为
的值为
A.2006 B.2007 C.2008 D.2009
12.如图,E、G、F、H分别是矩形ABCD四条边上的点,EF⊥GH,若AB=2,BC=3,则EF:GH=________.
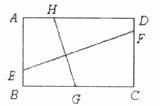
A.2:3 B.3:2 C.4:9 D.无法确定
二、填空题:(每题3分,共计30分)
13.当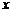 =________时,二次根式
=________时,二次根式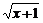 的值最小.
的值最小.
14.式子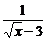 有意义的条件是________.
有意义的条件是________.
15.方程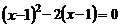 的根为________.
的根为________.
16.已知: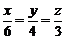 (
(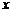 、
、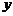 、
、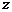 均不为零),则
均不为零),则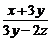 =________.
=________.
17.计算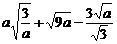 =________.
=________.
18.若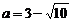 ,则代数式
,则代数式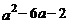 的值为________.
的值为________.
19.若最简二次根式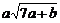 与
与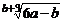 是同类二次根式,则
是同类二次根式,则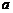 =________,
=________,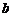 =________.
=________.
20.若实数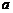 ,
,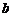 满足
满足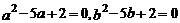 ,则
,则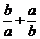 =________.
=________.
21.为应对金融危机,拉动内需,湖南省人民政府定今年为“湖南旅游年”。青年旅行社3月底组织赴凤凰古城、张家界风景区旅游的价格为每人1000元,为了吸引更多的人赴凤凰、张家界旅游,在4月底、5月底进行了两次降价,两次降价后的价格为每人810元,那么这两次降价的平均降低率为________.
22.根据指令[s,A](s≥0,0°<A<180°,机器人在平面上能完成下列动作:先在原地逆时针旋转角度A,再朝其面对的方向沿直线行走距离s,现机器人在平面直角坐标系的坐标原点,且面对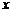 轴正方向.
轴正方向.
(1)若给机器人下了一个指令[4,30°],则机器人应移到点________;
(2)若机器人仍在原点,且面对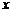 轴正方向,请你给机器人下一个指令________,使其移动到点(一2,2).
轴正方向,请你给机器人下一个指令________,使其移动到点(一2,2).
三、解答题(共计54分)
23.(本题满分6分)
已知关于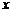 的方程
的方程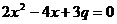 的一个根是
的一个根是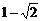 ,求方程的另一个根和
,求方程的另一个根和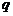 的值.
的值.
24.(本题满分8分)
己知代数式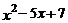 ,先用配方法说明,不论
,先用配方法说明,不论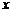 取何值,这个代数式的值总是正数;再求出当
取何值,这个代数式的值总是正数;再求出当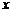 取何值时,这个代数式的值最小,最小值是多少?
取何值时,这个代数式的值最小,最小值是多少?
甲、乙两人同时解答题目:“化简并求值: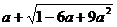 ,其中
,其中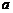 =5.”甲、乙两人的解答不同:
=5.”甲、乙两人的解答不同:
甲的解答是: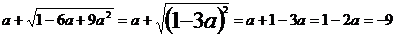 ;
;
乙的解答是: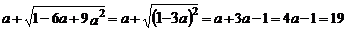 .
.
(1) ________的解答是错误的.
(2)错误的解答在于未能正确运用二次根式的性质:________.
(3)模仿上题解答:化简并求值: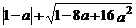 ,其中
,其中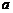 =2
=2
26.(本题满分10分)
关于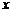 的方程
的方程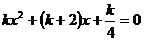 有两个不相等的实数根.
有两个不相等的实数根.
(1)求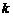 的取值范围.
的取值范围.
(2)是否存在实数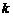 ,使方程的两个实数根的倒数和等于0?若存在,求出
,使方程的两个实数根的倒数和等于0?若存在,求出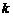 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
27.(本题满分10分)某服装厂为学校艺术团生产一批演出服,总成本3000元,售价每套30元.服装厂向24名家庭贫困学生免费提供.经核算,这24套演出服的成本正好是原定生产这批演出服的利润.问这批演出服共生产了多少套?
如图(1),在△ABC中,由DE∥BC,我们可以得到△ADE∽△ABC,从而有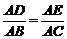 ,
,
即AD?AC=AE?AB,
于是AD?(AE+EC)=AE?(AD+DB),
AD?EC=AE?DB,
从而 ,
,
即△ABC中BC的平行线DE将另两条边AB、AC分割为成比例线段.
(1)如图(1),如果D是AB的中点,则E是________的中点,且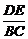 =________.
=________.
(2)如图(2),DE∥FG∥BC,AD=DF=FB,那么AE、EG、GC有什么关系?并说明理由.
(3)如图(3),DE∥FG∥BC,DF=FB,那么EG与GC有什么关系?并说明理由.