2008-2009学年度淄博市周村九年级中考二模
数学试卷
注意事项:
1.答题前请考生务必在答题卡及试卷的规定位置将自己的姓名、考试号、考试科目、座号等内容填写(涂)准确。
2.本试题分第Ⅰ卷和第Ⅱ卷两部分。第Ⅰ卷(1~4页)为选择题,36分;第Ⅱ卷(5~12页)为非选择题,84分;共120分。考试时间为120分钟。
3.第Ⅰ卷每小题选出答案后,必须用2B铅笔把答题卡上对应题目的答案标号(ABCD)涂黑。如需改动,须先用橡皮擦干净,再改涂其它答案。第Ⅱ卷须用蓝黑钢笔或圆珠笔直接答在试卷上。考试时,不允许使用计算器。
4.考试结束后,由监考教师把第Ⅰ卷(讲评用)和第Ⅱ卷及答题卡一并收回。
第Ⅰ卷(选择题 共36分)
一、选择题:本题共12小题,在每小题所给出的四个选项中,只有一个是正确的,请把正确的选项涂在答题卡的相应位置上。每小题3分,错选、不选或选出的答案超过一个,均记0分。
1.下列运算正确的是
A. B.
B.
C. D.
D.
2.下列各根式中与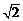 是同类二次根式的是
是同类二次根式的是
A. B.
B. C.
C. D.
D.
3.今年3月5日,温家宝总理在《政府工作报告》中,讲述了六大民生新亮点,其中之一就是全部免除了西部地区和部分中部地区农村义务教育阶段约52000000名学生的学杂费。这个数据保留两个有效数字用科学记数法表示为
A.52×107 B.5.2×
4.如图,是由一些相同的小正方体搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是
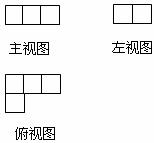
A.4 B.
5.在一个不透明的袋中装有2个红球和3个白球,它们除了颜色外都相同,从中随机摸出1个球,则摸出红球的概率是
A.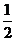 B.
B. C.
C.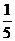 D.
D.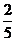
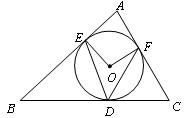
6.如图, O内切于
O内切于 ,切点分别为
,切点分别为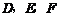 。已知
。已知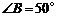 ,
,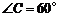 ,连接
,连接 ,那么
,那么 等于
等于
A. B.
B. C.
C. D.
D.
7.下列关于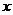 的一元二次方程中,有两个不相等的实数根的方程是
的一元二次方程中,有两个不相等的实数根的方程是
A.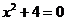 C.
C.
C. D.
D.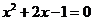
8.已知 ,且
,且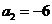 ,那么
,那么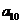 等于
等于
A. B.
B. C.
C.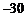 D.
D.
9.如图,如果从半径为 圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为
圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为
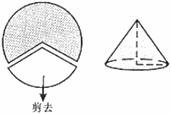
A. cm C.
cm C.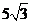 cm
cm
10.如图,矩形ABCD的边AB在x轴上,AB的中点与原点重合,AB=2,AD=1,过定点Q(0,2)和动点P(a,0)的直线与矩形ABCD的边有公共点,则a的取值范围是.

A.-2≤a≤2 B. -1≤a≤
11.函数 与
与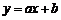 的图像只可能是( )
的图像只可能是( )
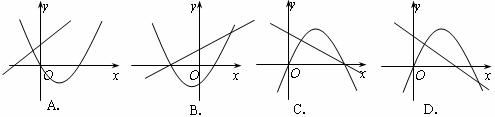
12.如图,有一张矩形纸片ABCD,AB=3,AD=4,现将纸片折叠,使C点与A点重合,则折痕EF的长为

A.15 B.12 C.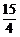 D. 5
D. 5
第Ⅱ卷(非选择题 共84分)
二、填空题:本题共5小题,满分20分.只要求填写最后结果,每小题填对得4分.
13.如图,直线AD与直线BE相交于点C, ,则∠OBE+∠ODA等于
,则∠OBE+∠ODA等于
度.

14.一个骰子连续投2次,点数和为4的概率是 .
15.一项调查统计情况如图所示,本次抽样的样本容量是__________.图中c=_________.若被调查的对象占总体数的20%,请根据样本估计总体中A类对应的数值为 .

17.如图,DE是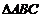 的中位线,M是DE的中点,CM的延长线交AB于N,那么
的中位线,M是DE的中点,CM的延长线交AB于N,那么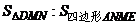 =_________________.
=_________________.

三、解答题:本大题共8小题,共64分.解答要写出必要的文字说明、证明过程或演算步骤.
18.(本题满分6分)
 ,并将其解集在数轴上表示出来.
,并将其解集在数轴上表示出来.
19.(本题满分6分)
小王、小李和小林三人准备打乒乓球,他们约定用“抛硬币”的方式来确定哪两个人先上场,三人手中各持有一枚质地均匀的硬币,同时将手中硬币抛落到水平地面为一个回合。落地后,三枚硬币中,恰有两枚正面向上或者反面向上的两人先上场;若三枚硬币均为正面向上或反面向上,属于不能确定。
(1)请你完成下图中表示“抛硬币”一个回合所有可能出现的结果的树状图;

(2)求一个回合能确定两人先上场的概率.
20.(本题满分8分)
已知二次函数 当
当 时,都有
时,都有 ,
,
当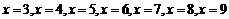 时,
时,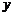 的值都是正整数,且
的值都是正整数,且 ,
,
求二次函数的解析式
21.(本题满分8分)
某渔民准备承包一块正方形水域围网养鱼,通过调查得知:在该正方形水域四周的围网费用平均每千米0.25万元,上交承包费、购买鱼苗、饲料和鱼药等开支每平方千米需0.5万元。政府为鼓励渔民发展水产养殖,每位承包户补贴0.5万元.预计每平方千米养的鱼可售得4.5万元.若该渔民期望养鱼当年获得净收益3.5万元,你应建议该渔民承包多大面积的水域?
22.(本题满分8分)
河岸边有一根电线杆AB(如下图),河岸距电线杆AB水平距离是14米,即BD=14米,该河岸的坡面CD的坡度 为
为 ,岸高CF为2米,在坡顶C处测得杆顶A的仰角为30°,D、E之间是宽2米的人行道,请你通过计算说明在拆除电线杆AB时,为确保安全,是否将此人行道封上?(提示:在地面上以点B为圆心,以AB长为半径的圆形区域为危险区域,
,岸高CF为2米,在坡顶C处测得杆顶A的仰角为30°,D、E之间是宽2米的人行道,请你通过计算说明在拆除电线杆AB时,为确保安全,是否将此人行道封上?(提示:在地面上以点B为圆心,以AB长为半径的圆形区域为危险区域, )
)

23.(本题满分8分)
如图(1),∠ABC=90°,O为射线BC上一点,OB = 4,以点O为圆心,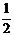 BO长为半径作⊙O交BC于点D、E。
BO长为半径作⊙O交BC于点D、E。
(1)当射线BA绕点B按顺时针方向旋转多少度时与⊙O相切?请说明理由.
(2)若射线BA绕点B按顺时针方向旋转与⊙O相交于M、N两点(如图(2)),MN= ,求的长.
,求的长.

24.(本题满分10分)
如图1,是美国总统Garfield于1876年给出的一种验证勾股定理的办法。Rt△ACB与Rt△DEB全等,点C、B、E共线,连接AD,可以证明△ABD是等腰三角形。如图2,Rt△ACB与Rt△DEB全等,点C、B、E共线,连接AD,交BC于点F,请你找出图2中的所有等腰直角三角形(不再添加线,不再添加字母),并给出证明。

25.(本题满分10分)
已知:在Rt△ABO中,∠OAB=90°,∠BOA=30°,AB=2,若以O为坐标原点,OA所在直线为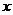 轴,建立如图所示平面直角坐标系,点B在第一象限内,将Rt△ABO沿OB折叠后,点A落在第一象限内的点C处.
轴,建立如图所示平面直角坐标系,点B在第一象限内,将Rt△ABO沿OB折叠后,点A落在第一象限内的点C处.
(1)求点C的坐标;
(2)若抛物线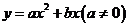 经过C、A两点,求此抛物线的解析式;
经过C、A两点,求此抛物线的解析式;
(3)若上述抛物线的对称轴与OB交于点D,点P为线段DB上一动点,过P作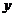 轴的平行线,交抛物线于点M,问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
轴的平行线,交抛物线于点M,问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由.

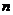
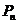
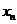 ,
,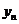
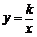 图象上的一列点,其中
图象上的一列点,其中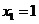 ,
,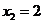 ,…,
,…,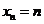
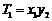 ,
,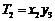 ,…,
,…,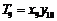 ;若
;若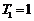 ,则
,则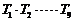 的值是______________.
的值是______________.