2008年通州区初三统一练习(一)
数学试卷
第 Ⅰ 卷 (选择题 32分)
一、选择题(共8个小题,每小题4分,共32分)在每个小题给出的四个备选答案中,只有一个是符合题目要求的.
1. -6的绝对值是
A. 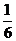 B.
-
B.
-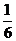 C.
6
D. -6
C.
6
D. -6
2. 我国最长的河流――长江全长约为6300千米,用科学记数法可表示为
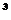 千米 B. 6.3×10
千米 B. 6.3×10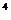 千米 C. 6.3×10
千米 C. 6.3×10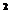 千米 D. 63×10
千米 D. 63×10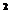 千米
千米
3.
在函数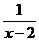 中,自变量x的取值范围是
中,自变量x的取值范围是
A. 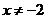 B.
B. 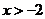 C.
C. 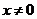 D.
D.
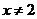
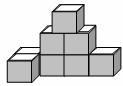
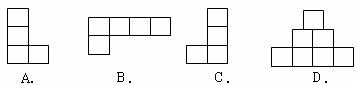
4. 下面的图形是由8个棱长为1个单位的小立方体组成的立体图形,这个立体图形的主视图是
5.
学校开展为贫困地区捐书活动,以下是5名同学捐书的册数:2,2,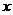 ,4,9.其中x是这组数中看不清的数字,但又知这组数据的平均数是4,则这组数据的中位数和众数分别是( )
,4,9.其中x是这组数中看不清的数字,但又知这组数据的平均数是4,则这组数据的中位数和众数分别是( )
A.2和2
B.4和
6.小明根据下表,作了三个推测:
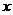
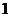
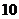
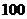
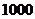
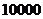
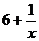
7
6.1
6.01
6.001
6.0001
①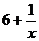 (x >0)的值随着
(x >0)的值随着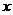 的增大越来越小;②
的增大越来越小;②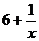 (x >0)的值有可能等于
(x >0)的值有可能等于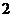 ;
;
③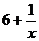 (x >0)的值随着
(x >0)的值随着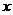 的增大越来越接近于
的增大越来越接近于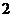 .其中,推测正确的有
.其中,推测正确的有
A.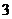 个 B.
个 B.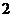 个 C.
个 C.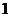 个 D.
个 D.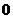 个
个
7. 如图, AB是⊙O的直径, CD是弦, 且CD⊥AB, 若BC=8, AC=6, 则sin∠ABD的值为
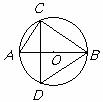
A.  B.
B.
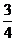 C.
C.
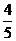 D.
D.
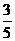
8.
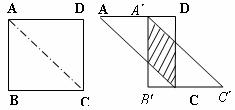
如图,将边长为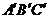 ?,若两个三角形重叠部分的面积是
?,若两个三角形重叠部分的面积是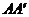 ?等于
?等于
第Ⅱ卷 (非选择题 88分)
二、填空题(共4个小题 , 每小题4分,共16分)
9. 点A(-1,y1),B(-3,y2)在双曲线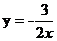 上, 则y1与y2的大小关系是____________.
上, 则y1与y2的大小关系是____________.
10. 有两张背面相同的纸牌,其正面分别是三角形和圆,将这两张纸牌背面朝上随机摸出一张,放回后,再随机摸出一张.两次摸出都是圆的概率是__________.
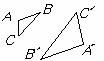
11. 如图,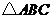 与
与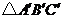 是位似图形,且位似比是
是位似图形,且位似比是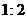 ,若AB=
,若AB=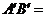
cm .
12.观察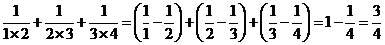 依照此法计算
依照此法计算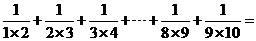 .
.
三、(共3个小题,其中13小题4分,14、15小题每小题5分,共14分)
13.分解因式: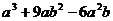 .
.
14.
计算: 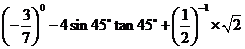
15.解方程: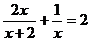 .
.
四、(共4个小题, 每小题5分,共20分)
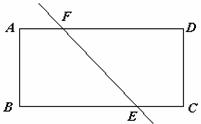
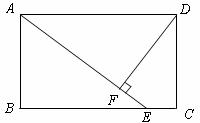
16. 已知:如图,四边形ABCD是矩形(AD>AB),点E在BC上,且AE =AD,DF⊥AE,垂足为F. 请探求DF与AB有何数量关系?写出你所得到的结论并给予证明.
17.某超级市场销售一种计算器,每个售价48元.后来,计算器的进价降低了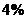 ,但售价未变,从而使超市销售这种计算器的利润率提高了
,但售价未变,从而使超市销售这种计算器的利润率提高了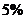 .这种计算器原来每个进价是多少元?(利润
.这种计算器原来每个进价是多少元?(利润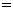 售价
售价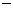 进价,利润率
进价,利润率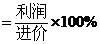 )
)
18.
如图,在一次数学活动课上,老师带领学生去测教学楼的高度.在阳光下,测得身高 )的影长(
)的影长(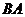 )为
)为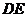 的影长
的影长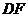 为
为
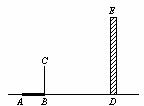
(1)请你在图中画出此时教学楼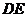 在阳光下的投影
在阳光下的投影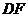 ;
;
(2)请你根据已测得的数据,求出教学楼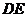 的高度(精确到
的高度(精确到
19.
如图,点 在⊙O上,
在⊙O上,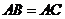 ,
,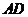 与
与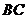 相交于点
相交于点 ,
,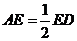 ,延长
,延长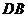 到点
到点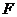 ,使
,使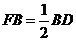 ,连结
,连结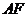 .
.
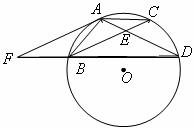
(1)证明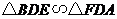 ;
;
(2)试判断直线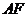 与⊙O的位置关系,并给出证明.
与⊙O的位置关系,并给出证明.
五、(共3个小题,每小题5分,共15分)
20.
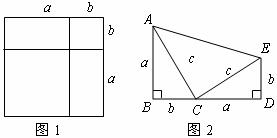
(1)如图1是一个重要公式的几何解释.请你写出这个公式;
(2)如图2, ,
,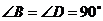 ,且
,且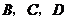 三点共线.
三点共线.
试证明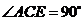 ;
;
(3)请利用(1)中的公式和图2证明勾股定理.
21. 某中学为了培养学生的社会实践能力,要求学生参加一项社会调查活动.为此,小明在他所居住小区的600个家庭中,随机调查了50个家庭的月收入情况,并绘制了如下的频数分布表和频数分布直方图(收入取整数,单位:元).
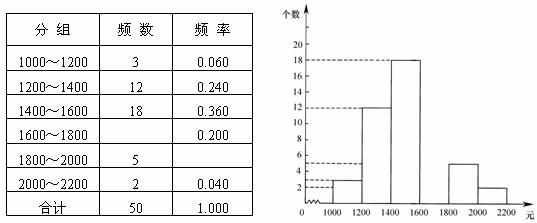
请你根据以上提供的信息,解答下列问题:
(1)补全频数分布表和频数分布直方图;
(2)这50个家庭收入的中位数落在 小组;
(3)请你估算该小区600个家庭中收入较低(不足1400元)的家庭个数大约有多少?
22. 如图,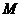 是边长为4的正方形
是边长为4的正方形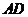 边的中点,动点
边的中点,动点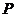 自
自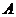 点起,由
点起,由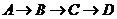 匀速运动,直线
匀速运动,直线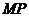 扫过正方形所形成的面积为
扫过正方形所形成的面积为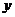 ,点
,点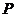 运动的路程为
运动的路程为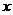 ,请解答下列问题:
,请解答下列问题:
(1)当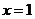 时,求
时,求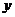 的值;
的值;
(2)就下列各种情况,求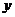 与
与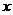 之间的函数关系式;
之间的函数关系式;
①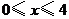 ;②
;②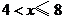 ;③
;③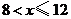 ;
;
(3)在给出的直角坐标系中,画出(2)中函数的图象.
六、(本题满分7分)
23. 从有关方面获悉,在我国农村已经实行了新型农村合作医疗保险制度,享受医保的农民可在规定的医院就医并按规定标准报销部分医疗费用,下表是医疗费用报销的标准:
医疗费用范围
门诊
住院
0-5000元
5001-20000元
20000元以上
每年报销比例标准
30%
30%
40%
50%
(说明:住院医疗费用的报销分段计算.如:某人住院医疗费用共30000元,则5000元
按30%报销、15000元按40%报销、余下的10000元按50%报销;题中涉及到的医疗费均指允许报销的医疗费).
(1)某农民在2006年门诊看病自己共报销医疗费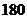 元,则他在这一年中门诊医疗费用共
元,则他在这一年中门诊医疗费用共
元;
(2)设某农民一年中住院的实际医疗费用为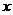 元(
元(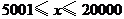 ),按标准报销的金额为
),按标准报销的金额为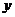 元,试求出
元,试求出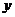 与
与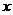 的函数关系式;
的函数关系式;
(3)若某农民一年内本人自负住院医疗费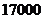 元(自负医疗费=实际医疗费
元(自负医疗费=实际医疗费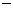 按标准报销的金额),则该农民当年实际医疗费用共多少元?
按标准报销的金额),则该农民当年实际医疗费用共多少元?
七、(本题满分8分)
24. 如图,已知与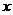 轴交于点
轴交于点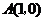 和
和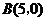 的抛物线
的抛物线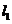 的顶点为
的顶点为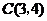 ,抛物线
,抛物线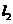 与
与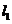 关于
关于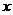 轴对称,顶点为
轴对称,顶点为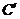 .
.
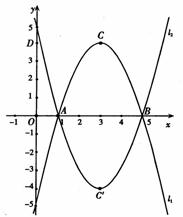
(1)求抛物线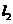 的函数关系式;
的函数关系式;
(2)已知原点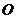 ,定点
,定点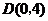 ,
,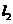 上的点
上的点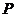 与
与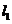 上的点
上的点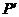 始终关于
始终关于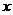 轴对称,则当点
轴对称,则当点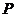 运动到何处时,以点
运动到何处时,以点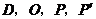 为顶点的四边形是平行四边形?
为顶点的四边形是平行四边形?
(3)设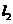 上的点M、N分别与
上的点M、N分别与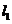 上的点
上的点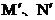 始终关于x轴对称.是否存在点
始终关于x轴对称.是否存在点 、N(M在N的左侧),使四边形MNN´M´是正方形?若存在,求出点
、N(M在N的左侧),使四边形MNN´M´是正方形?若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
|