2007年烟台市海阳初中四年级摸底考试
数学试卷
说明:
1.本试题分为I卷和Ⅱ卷两部分,第I卷为选择题,第Ⅱ卷为非选择题。考试时间120分钟,满分150分。
2.答题前将密封线内的项目填写清楚,考试结束后,只交第Ⅱ卷和答题卡。
第I卷
注意事项:
1.使用答题卡的考生,请考生将自己的姓名、考号、考试科目、试卷类型(A)涂写在答题卡上。选择题选出答案后,用2B铅笔把答题卡对应题目的答案标号涂黑,不能答在本试题上。如要改动,必须先用橡皮擦干净,再选涂另一个答案。
2.不使用答题卡的考生,请考生将选择题答案填写在第Ⅱ卷上的答题表中。
一、选择题(本题共12个小题,每小题4分,满分48分)每小题都给出标号为A、B、C、D四个备选答案。其中有且只有一个是正确的。
1.我省今年加大公路建设投入,年底全省公路总里程将达到208000千米。若用科学记数法表示,且四舍五入保留2个有效数字,则208000可表示为
A.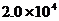 B.
B.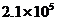 C.
C.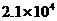 D.
D.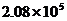
2.有下列运算:
①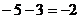 ; ②
; ②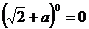 ; ③
; ③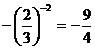 ; ④
; ④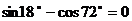
其中运算结果正确的是
A.③④ B.②③④ C.②④ D.①②③④
3.如果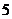 是
是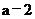 的相反数,那么
的相反数,那么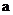 的值是
的值是
A.-5 B.
4.在数轴上表示不等式组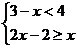 的解集,正确的是
的解集,正确的是
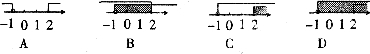
5.下图是由一些完全相同的小立方块搭成的几何体的三种视图,那么搭成这个几何体所用的小立方块的个数是
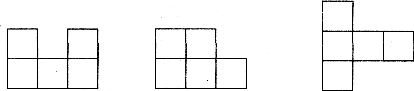
主视图 左视图 俯视图
A.7个 B.8个 C.9个 D.7个或8个
6.国家为九年义务教育期间的学生实行“两免一补”政策,下表是西部某市某中学国家免费提供教科书补助的部分情况:
项目 年级
七
八
九
合计
每人免费补助金额(元)
110
90
50
人数(人)
80
300
免费补助总金额(元)
4000
26200
如果要知道空白处的数据,可设七年级的人数为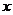 ,八年级的人数为
,八年级的人数为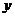 ,根据题意列出方程组为
,根据题意列出方程组为
A.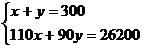 B.
B. 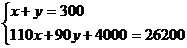
C.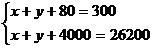 D.
D.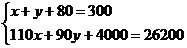
7.一桌上有容器口为正三角形、正方形、邻边不等的长方形、圆形的四个柱形容器(如图),若四个容器口的周长相同,容器的容积也相同,容器材料相同,且都装满了同一温度的水。则水蒸发较快的容器是
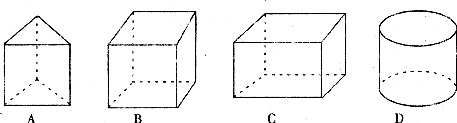
8.向阳中学初四?五班在一次考试中,50名学生的数学成绩如下:
分数
58
60
67
70
77
80
84
90
96
100
人数
2
3
4
5
l l
2
5
10
4
4
则此班学生成绩的众数、中位数分别是
A.77,77 B.77,
9.如图,方格纸上有 ,下列说法不正确的是
,下列说法不正确的是
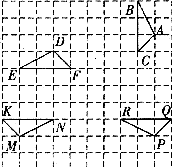
A.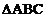 以
以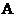 点为中心,逆时针方向旋转90°,再向左平移六格,向下平移一格,可变换成
点为中心,逆时针方向旋转90°,再向左平移六格,向下平移一格,可变换成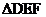
B.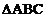 以
以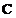 点为中心,顺时针方向旋转90°,再向左平移一格,向下平移四格,可变换成
点为中心,顺时针方向旋转90°,再向左平移一格,向下平移四格,可变换成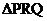
C.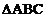 以
以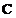 点为中心,顺时针方向旋转90°,再向左平移八格,向下平移四格,可变换成
点为中心,顺时针方向旋转90°,再向左平移八格,向下平移四格,可变换成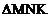
D.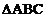 以
以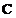 点为中心,逆时针方向旋转90°,再向左平移四格,向下平移一格,可变换成
点为中心,逆时针方向旋转90°,再向左平移四格,向下平移一格,可变换成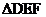
10.已知直线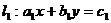 与直线
与直线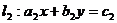 的交点为
的交点为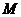 ,则直线
,则直线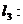
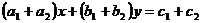 与
与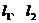 的关系是
的关系是
A.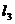 可能与
可能与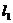 相交,但与
相交,但与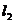 不相交
不相交
B.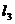 可能与
可能与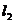 相交,但与
相交,但与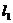 不相交
不相交
C.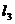 可能与
可能与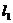 、
、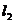 都相交,但
都相交,但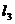 不过
不过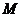 点
点
D.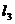 与
与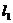 、
、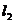 相交于
相交于 点
点
l1.一般家庭用电量(千瓦时)与气温(℃)有一定的关系,如图所示:图(1)表示某年12个月的月平均气温图,图(2)表示某家庭在这年12个月中每个月的用电量,根据这些信息,以下关于该家庭的用电量与其气温间关系的叙述中,正确的是
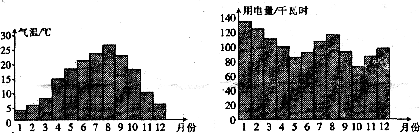
A.气温最高时,用电量最多
B.气温最低时,用电量最少
C.当气温小于
D.当气温高于
12.已知抛物线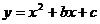 与
与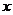 轴有两个交点,且都在
轴有两个交点,且都在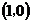 点右边,则下列说法:
点右边,则下列说法:
①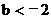 ;②
;②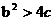 ;③
;③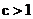 ;④
;④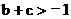
其中正确的有
A.4个 B.3个 C.2个 D.1个
第Ⅱ卷
二、填空题(本题共6个小题。每小题4分,满分24分)
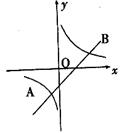
13.如图,一次函数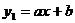 的图象与反比例函数
的图象与反比例函数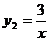 的图象相交于
的图象相交于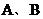 两点,当
两点,当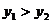 时,
时,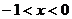 或
或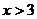 ,则一次函数的解析式为
。
,则一次函数的解析式为
。
14.在平面直角坐标系中,过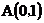 与
与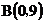 两点,且与
两点,且与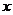 轴正半轴相切的圆的圆心坐标为
。
轴正半轴相切的圆的圆心坐标为
。
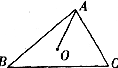
15.如图,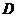 是
是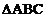 的外心,
的外心,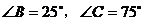 ,则
,则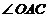 的度数为 。
的度数为 。
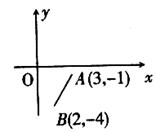
16.已知点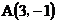 、点
、点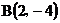 ,平移线段
,平移线段 ,使其端点分别落在
,使其端点分别落在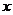 轴的
轴的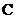 点和
点和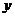 轴的
轴的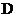 点,则
点,则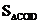 =
。
=
。
17.如图,有一长度为

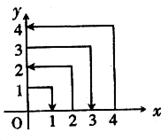
18.如图所示一个质点在第一象限内及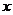 轴、
轴、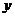 轴上运动,在第一秒内它由原点移动到
轴上运动,在第一秒内它由原点移动到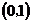 点,而后接着按图所示在
点,而后接着按图所示在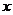 轴,
轴,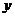 轴平行的方向运动,且每秒移动一个单位长度,那么质点运动到点
轴平行的方向运动,且每秒移动一个单位长度,那么质点运动到点 (
(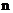 为正整数)的位置时,用代数式表示所用的时间为
秒。
为正整数)的位置时,用代数式表示所用的时间为
秒。
三、解答题(本题共有2个小题,第19题5分,第20题8分,满分13分)
19.解方程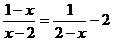
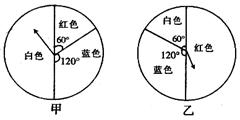
20.李明、张欣、杨武三同学都想参加学校组织的周末社会活动,而又只能参加一人,三位同学采用了两个转盘定人选的方法:
如图,规定同时转动甲乙两个转盘,两指针指向同一色为准(若指针指向分界线或不同色,重转),每人选一色,先转出的胜出。
三位同学思考片刻后,杨武选了蓝色,李明选了红色,而张欣选了白色。
你认为三同学胜出的机会相同吗?若不同,请说明哪位同学胜出的可能性较大;若机会相同,请说明理由。
四、解答题(本题满分9分)
21.受台风的影响,一电线杆向西北方向倾斜了,初四?三班的数学小组要测一下此电线杆地上部分的长度。他们在电线杆的影子恰好指向西北方向时,测得电线杆的影子长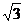 取1.73)。
取1.73)。
五、解答题(本题满分9分)
22.某公司经营某种电子琴和洗衣机,市场需求量较大,每销售出一台电子琴,公司用于劳动力的投入500元,用于其他方面成本投入3000元,每销售出一台洗衣机,公司用于劳动力的投入1000元,用其他方面成本投入2000元。某月公司计划供应这两种产品12台。且用于劳动力的投入不超过1.1万元,用于其他方面成本投入不超过3万元。
(1)请你根据要求,设计出该月电子琴和洗衣机的供应方案;
(2)若每销售出一台电子琴和洗衣机公司获得的利润分别为600元和800元,则该月公司选择(1)中哪个方案可获得最大利润,最大利润是多少?
六、解答题(本题满分10分)
23.如图,边长为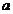 的正方形
的正方形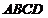 的中心为
的中心为 ,
,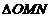 中,
中,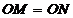 ,且
,且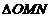 绕点
绕点 旋转时,能依次覆盖正方形各顶点(即各顶点在
旋转时,能依次覆盖正方形各顶点(即各顶点在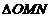 内)。
内)。
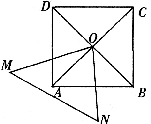
(1)当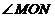 为多少度时,
为多少度时,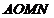 覆盖的正方形部分的面积始终为正方形面积的
覆盖的正方形部分的面积始终为正方形面积的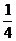 ?并说明理由;
?并说明理由;
(2)求满足(1)的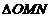 的面积的最小值;
的面积的最小值;
(3)若将条件中正方形换成正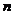 边形,其他条件不变,那么
边形,其他条件不变,那么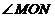 为多少度时,
为多少度时,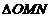 覆盖的正
覆盖的正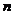 边形的面积始终为正
边形的面积始终为正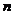 边形的
边形的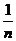 ?这样的
?这样的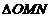 的面积最小值为多少?(要求:只写出结果,不写解答过程)
的面积最小值为多少?(要求:只写出结果,不写解答过程)
七、解答题(本题满分11分)
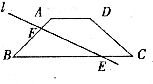
24.在等腰梯形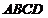 中,
中,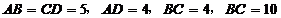 ,一条直线
,一条直线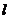 与下底
与下底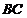 相交于点
相交于点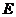 ,且直线
,且直线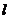 将等腰梯形
将等腰梯形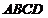 的周长平分。
的周长平分。
(1)如图,若直线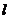 与腰
与腰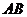 相交于点
相交于点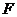 ,设
,设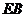 为
为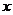 ,试用含
,试用含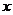 的代数式表示
的代数式表示 的面积;
的面积;
(2)是否存在直线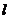 将等腰梯形
将等腰梯形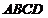 的周长和面积同时平分?若存在,指出符合要求的所有直线的特征;若不存在,请说明理由。
的周长和面积同时平分?若存在,指出符合要求的所有直线的特征;若不存在,请说明理由。
八、解答题(本题满分12分)
25.在正方形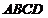 中,
中,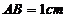 ,点
,点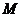 是
是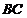 (端点除外)上一个动点,以
(端点除外)上一个动点,以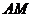 为边作正方形
为边作正方形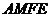 ,连接
,连接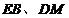 。
。
(1)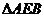 的面积是否变化?若不变化,请求出其面积;若变化,请说明理由。
的面积是否变化?若不变化,请求出其面积;若变化,请说明理由。
(2)探究: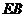 与
与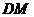 的关系。
的关系。
(3)点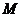 在何处时四边形
在何处时四边形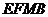 的面积最小?最小值是多少?
的面积最小?最小值是多少?
九、解答题(本题满分14分)
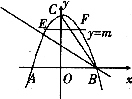
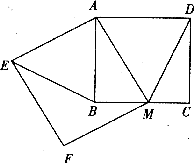
26.如图,已知点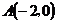 ,直线
,直线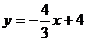 交
交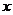 轴于点
轴于点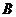 ,交
,交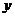 轴于点
轴于点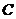
(1)求对称轴平行于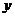 轴,且过
轴,且过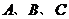 三点的抛物线解析式;
三点的抛物线解析式;
(2)若直线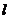 平分∠ABC,求直线
平分∠ABC,求直线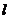 的解析式;
的解析式;
(3)若直线产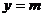 (
(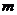 >0)交(1)中抛物线于
>0)交(1)中抛物线于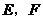 两点,问:
两点,问: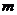 为何值时,以
为何值时,以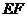 为边的正方形的面积为9?
为边的正方形的面积为9?