摘要:(1)如图.若直线与腰相交于点.设为.试用含的代数式表示的面积,
网址:http://m.1010jiajiao.com/timu_id_668350[举报]
 如图,在平面直角坐标系xOy中,已知点A(a,0)(a>0),B(2,3),C(0,3).过原点O作直线l,使它经过第一、三象限,直线l与y轴的正半轴所成角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,我们把这个操作过程记为FZ[θ,a].
如图,在平面直角坐标系xOy中,已知点A(a,0)(a>0),B(2,3),C(0,3).过原点O作直线l,使它经过第一、三象限,直线l与y轴的正半轴所成角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,我们把这个操作过程记为FZ[θ,a].(Ⅰ)若点D与点A重合,则θ=
(Ⅱ)若θ=45°,点B落在点E处,若点E在四边形0ABC的边AB上,求点A的坐标;
(Ⅲ)作直线CD交x轴于点G,交直线AB于点H,使得△ODG与△GAH是一对相似的等腰三角形,直接写出a的值.
 如图,已知抛物线
如图,已知抛物线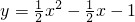 与x轴相交于点A、B,与y轴相交于C.
与x轴相交于点A、B,与y轴相交于C.
(1)求点A、B、C的坐标及直线BC的解析式;
(2)设抛物线的顶点为点D,求△ACD的面积S
(3)在直线BC上是否存在一点P,使△ACP是以AC为一腰的等腰三角形?若存在,求点P的坐标;若不存在,说明理由.
查看习题详情和答案>>
如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC = 4,AB边上有一动点P(不与A、B重合),连结DP,作PQ⊥DP,使得PQ交射线BC于点E,设AP=x.
1.当x为何值时,△APD是等腰三角形?
2.若设BE=y,求y关于x的函数关系式
3.若BC的长可以变化,在现在的条件下,是否存在点P,使得PQ经过点C?若存在,求出相应的AP的长;若不存在,请说明理由,并直接写出当BC的长在什么范围内时,可以存在这样的点P,使得PQ经过点C.

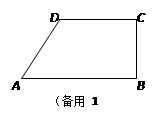

查看习题详情和答案>>
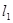 交直线
交直线
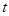 为何值时,
为何值时,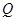 是
是