2006―2007学年度广西南宁二中、桂林中学、玉林高中高三年级三校联考
数学(理)试题
一、单项选择题(每小题5分,共60分)
1.已知全集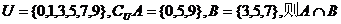 = ( )
= ( )
 A.{5,7} B.{3,7} C.{3,5,7} D.
A.{5,7} B.{3,7} C.{3,5,7} D.
2.条件甲: ( )
( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既充分也不必要条件
3.函数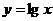 的图象绕过原点逆时针旋转90°后得到新的图象F,则F所表示的函数是
的图象绕过原点逆时针旋转90°后得到新的图象F,则F所表示的函数是
( )
A.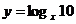 B.
B. C.
C. D.
D.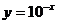
4.等比数列 的首项为1,公比为q,前n项和为S,则数列
的首项为1,公比为q,前n项和为S,则数列 项之和为( )
项之和为( )
A. B.S C.
B.S C. D.
D.
5.在 的形状一定是 ( )
的形状一定是 ( )
A.正三角形 B.直角三角形 C.锐角三角形 D.钝角三角形
6.函数 的图象的一个对称中心是 ( )
的图象的一个对称中心是 ( )
A. B.
B. C.
C. D.
D.
7.设复数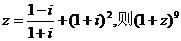 的二项展开式的第7项是 ( )
的二项展开式的第7项是 ( )
A.-84 B.-84i C.36 D.-36i
8.已知函数 所形成区域的面积为
所形成区域的面积为
( )
|
 B.
B. C.
C. D.
D.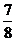
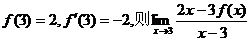 的值为 ( )
的值为 ( )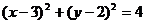 上,左准线为y轴,则该椅椭圆的离心率e的取值范围是 ( )
上,左准线为y轴,则该椅椭圆的离心率e的取值范围是 ( ) B.
B. C.
C. D.
D.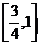
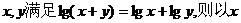 为自变量的函数y的单调递减区间是
为自变量的函数y的单调递减区间是 且
且
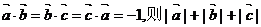 =
.
=
.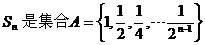 的所有3元子集的元素和之和,则
的所有3元子集的元素和之和,则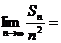
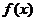 是奇函数,且在定义域(-1,1)内可导,并满足
是奇函数,且在定义域(-1,1)内可导,并满足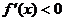 ,解关于m的不等式
,解关于m的不等式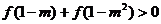 .
.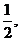 若每局比赛组织者可获利100万美元,设各局比赛的相互间没有影响.组织者在本次比赛获利
若每局比赛组织者可获利100万美元,设各局比赛的相互间没有影响.组织者在本次比赛获利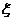 万美元,求
万美元,求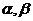 是同一个三角形的两角,且
是同一个三角形的两角,且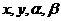 之间满足不下列关系
之间满足不下列关系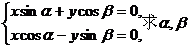 的值.
的值.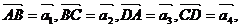 且
且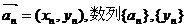 分别是等差数列和等比数列,求证:四边形ABCD是平行四边形.
分别是等差数列和等比数列,求证:四边形ABCD是平行四边形.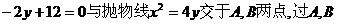 两点与圆M与抛物线交在A处有公共的切线.
两点与圆M与抛物线交在A处有公共的切线.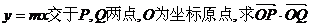 的值.
的值. 中,
中,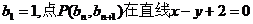 上.
上.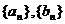 的通项公式
的通项公式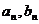 ;
;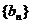 的前n项为
的前n项为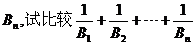 与2的大小;
与2的大小; 的最小整数c.
的最小整数c.



 是减函数.
是减函数.





 表示本次比赛组织者可获利400万美元,既本次比赛马刺队(或活塞队)
表示本次比赛组织者可获利400万美元,既本次比赛马刺队(或活塞队)
 表示本次比赛组织者可获利500万美元,即本次比赛马刺队(或活塞队)
表示本次比赛组织者可获利500万美元,即本次比赛马刺队(或活塞队)





 万美元.
万美元.





 ,
,







 抛物线在A处的切线斜率y′=3,设圆的方程为
抛物线在A处的切线斜率y′=3,设圆的方程为 .①
.① ②
② .
.
 .
.
 ,
,





 为的等比数列,
为的等比数列,



 为的等差数列,
为的等差数列,



 ①
①
 ②
②



