摘要:22.已知数列中.上.
网址:http://m.1010jiajiao.com/timu_id_31158[举报]
一、单项选择题(每小题5分,共60分)
1.B 2.B 3.D 4.C 5.C 6.D 7.A 8.D 9.B
10.C 11.B 12.A
二、填空题(每小题4分,共16分)
13.
14.
15.1
16.
三、解答题(本大题共6小题,共74分)
17.解:
 是减函数.
是减函数.

又由



18.解:
 表示本次比赛组织者可获利400万美元,既本次比赛马刺队(或活塞队)
表示本次比赛组织者可获利400万美元,既本次比赛马刺队(或活塞队)
以4:0获胜,所以
 表示本次比赛组织者可获利500万美元,即本次比赛马刺队(或活塞队)
表示本次比赛组织者可获利500万美元,即本次比赛马刺队(或活塞队)
以4:1获胜,所以
同理
故的概率分布为

400
500
600
700




 万美元.
万美元.
19.解:由
平方相加得
此时
再平方相加得


即 ,
,
结合
20.解:

又

(
故

∴四边形ABCD为两组对边相等的四边形.
故四边形ABCD是平行四边形.
21.解:
(1)由 抛物线在A处的切线斜率y′=3,设圆的方程为
抛物线在A处的切线斜率y′=3,设圆的方程为 .①
.①
又圆心在AB的中垂线上,即 ②
②
由①②得圆心 .
.
(2)联立直线与圆的方程得
即 .
.

22.解:
(1)由题意得 ,
,






 为的等比数列,
为的等比数列,
点


 为的等差数列,
为的等差数列,
(2)


(3) ①
①
当
当 ②
②
由①―②得 




已知数列![]() 中,
中,![]() 在直线
在直线![]() 上,其中
上,其中![]()
(I)令![]() 求证数列
求证数列![]() 是等比数列;
是等比数列;
(Ⅱ)求数列![]() 的通项;
的通项;
已知数列![]() 中,
中,![]() 且点
且点![]() 在直线
在直线![]() 上.
上.
(1)求数列![]() 的通项公式;
的通项公式;
(2![]() )若函数
)若函数![]()
求函数![]() 的最小值;
的最小值;
(3)设![]() 表示数列
表示数列![]() 的前
的前![]() 项和.试问:是否存在关于
项和.试问:是否存在关于![]() 的整式
的整式![]() ,使得
,使得
![]() 对于一切不小于2的自然数
对于一切不小于2的自然数![]() 恒成立? 若存在,写出
恒成立? 若存在,写出![]() 的解析式,并加以证明;若不存在,试说明理由。
的解析式,并加以证明;若不存在,试说明理由。
 已知数列
已知数列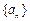 中,
中,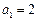 ,且
,且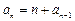
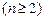 ,求这个数列的第m项
,求这个数列的第m项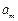 的值
的值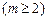 .现给出此算法流程图的一部分如图1,
.现给出此算法流程图的一部分如图1,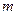 的值是多少?
的值是多少?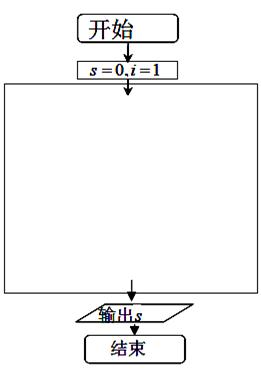
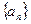 中,
中,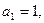 且点
且点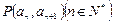 在直线
在直线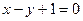 上.
上.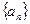 的通项公式;
的通项公式;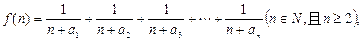
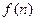 的最小值;
的最小值;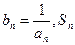 表示数列
表示数列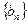 的前
的前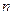 项和.试问:是否存在关于
项和.试问:是否存在关于 ,使得
,使得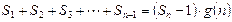 对于一切不小于2的自然数
对于一切不小于2的自然数