摘要：14．设O.A.B.C为平面内四个点.且
网址：http://m.1010jiajiao.com/timu_id_31148[举报]
一、单项选择题（每小题5分，共60分）
1．B 2．B 3．D 4．C 5．C 6．D 7．A 8．D 9．B
10．C 11．B 12．A
二、填空题（每小题4分，共16分）
13．
14．
15．1
16．
三、解答题（本大题共6小题，共74分）
17．解：
是减函数.
又由
18．解：
表示本次比赛组织者可获利400万美元，既本次比赛马刺队（或活塞队）
以4：0获胜，所以
表示本次比赛组织者可获利500万美元，即本次比赛马刺队（或活塞队）
以4：1获胜，所以
同理
故的概率分布为
400
500
600
700
万美元.
19．解：由
平方相加得
此时
再平方相加得
即
，
结合
20．解：
又
（
故
∴四边形ABCD为两组对边相等的四边形.
故四边形ABCD是平行四边形.
21．解：
（1）由
抛物线在A处的切线斜率y′=3，设圆的方程为
.①
又圆心在AB的中垂线上，即
②
由①②得圆心
.
（2）联立直线与圆的方程得
即
.
22．解：
（1）由题意得
，
为的等比数列，
点
为的等差数列，
（2）
（3）
①
当
当
②
由①―②得 
在A、B、C、D四小题中只能选做2题，每小题10分，共计20分，请在答题纸指定区域内作答，解答应写出文字说明、证明过程或演算步骤．A．选修4-1：（几何证明选讲）
如图，从O外一点P作圆O的两条切线，切点分别为A，B，
AB与OP交于点M，设CD为过点M且不过圆心O的一条弦，
求证：O，C，P，D四点共圆．
B．选修4-2：（矩阵与变换）
已知二阶矩阵M有特征值λ=3及对应的一个特征向量e1=[
1 1 |
C．选修4-4：（坐标系与参数方程）
在极坐标系中，曲线C的极坐标方程为p=2
| 2 |
| π |
| 4 |
|
D．选修4-5（不等式选讲）
已知实数x，y，z满足x+y+z=2，求2x2+3y2+z2的最小值．
[选做题]在A、B、C、D四小题中只能选做2题，每小题10分，计20分．请把答案写在答题纸的指定区域内．A．（选修4-1：几何证明选讲）
如图，圆O的直径AB=8，C为圆周上一点，BC=4，过C作圆的切线l，过A作直线l的垂线AD，D为垂足，AD与圆O交于点E，求线段AE的长．
B．（选修4-2：矩阵与变换）
已知二阶矩阵A有特征值λ1=3及其对应的一个特征向量α1=
|
|
C．（选修4-4：坐标系与参数方程）
以平面直角坐标系的原点O为极点，x轴的正半轴为极轴，建立极坐标系（两种坐标系中取相同的单位长度），已知点A的直角坐标为（-2，6），点B的极坐标为(4，
| π |
| 2 |
| π |
| 4 |
D．（选修4-5：不等式选讲）
设a，b，c，d都是正数，且x=
| a2+b2 |
| c2+d2 |
| (ac+bd)(ad+bc) |
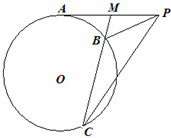
（1）自圆O外一点P引切线与圆切于点A，M为PA中点，过M引割线交圆于B，C两点．求证：∠MCP=∠MPB．（2）在平面直角坐标系xOy中，已知四边形ABCD的四个顶点A（0，1），B（2，1），C（2，3），D（0，2），经矩阵M=
|
（3）已知A是曲线ρ=12sinθ上的动点，B是曲线ρ=12cos(θ-
| π |
| 6 |
（4）设p是△ABC内的一点，x，y，z是p到三边a，b，c的距离，R是△ABC外接圆的半径，证明
| x |
| y |
| z |
| 1 | ||
|
| a2+b2+c2 |
（1）自圆O外一点P引切线与圆切于点A，M为PA中点，过M引割线交圆于B，C两点．求证：∠MCP=∠MPB．
（2）在平面直角坐标系xOy中，已知四边形ABCD的四个顶点A（0，1），B（2，1），C（2，3），D（0，2），经矩阵M=
表示的变换作用后，四边形ABCD变为四边形A1B1C1D1，问：四边形ABCD与四边形A1B1C1D1的面积是否相等？试证明你的结论．
（3）已知A是曲线ρ=12sinθ上的动点，B是曲线ρ=12cos(θ-
)上的动点，试求AB的最大值．
（4）设p是△ABC内的一点，x，y，z是p到三边a，b，c的距离，R是△ABC外接圆的半径，证明
+
+
≤
．
查看习题详情和答案>>
（2）在平面直角坐标系xOy中，已知四边形ABCD的四个顶点A（0，1），B（2，1），C（2，3），D（0，2），经矩阵M=
|
（3）已知A是曲线ρ=12sinθ上的动点，B是曲线ρ=12cos(θ-
| π |
| 6 |
（4）设p是△ABC内的一点，x，y，z是p到三边a，b，c的距离，R是△ABC外接圆的半径，证明
| x |
| y |
| z |
| 1 | ||
|
| a2+b2+c2 |
如图，在三棱锥S-ABC中，侧面SAB⊥底面ABC，且∠ASB=∠ABC=90°，AS=SB=2，AC=2| 3 |
（Ⅰ）求证SA⊥SC；
（Ⅱ）在平面几何中，推导三角形内切圆的半径公式r=
| 2S |
| l |
①以内切圆的圆心O为顶点，将三角形ABC分割成三个小三角形：△OAB，△OAC，△OB
C．②设△ABC三边长分别为a，b，c．由S△ABC=S△OBC+S△OAC+S△OAB，
得S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2S |
| l |
类比上述方法，请给出四面体内切球半径的计算公式（不要求说明类比过程），并利用该公式求出三棱锥S-ABC内切球的半径． 查看习题详情和答案>>