岳阳市一中2009年上期高三第七次考试
文科数学
时量:120 分钟 分值:150分 命题人:秦玉琴
一、选择题。(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 若集合M=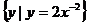 ,N=
,N=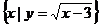 ,那么
,那么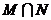 为 ( B )
为 ( B )
A.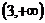 B.
B.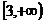 C.
C.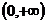 D.
D.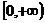
2. 函数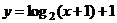 (x>0)的反函数为( A )
(x>0)的反函数为( A )
A.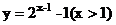 B.
B.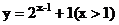 C.
C.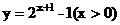 D.
D.
3. 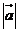 +
+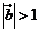 是
是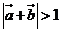 的
( B )
的
( B )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
4.设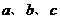 表示三条直线,
表示三条直线, 表示两个平面,则下列命题中逆命题不成立的是( C )
表示两个平面,则下列命题中逆命题不成立的是( C )
A.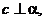 若
若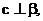 则
则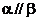 B.
B. 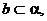
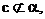 若
若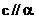 ,则
,则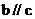
C.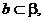 若
若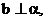 则
则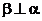 D.
D. 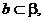 c是
c是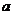 在
在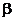 内的射影,若
内的射影,若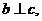 则
则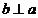
5. 在等差数列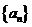 中,已知
中,已知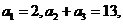 则
则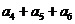 等于 ( B
)
等于 ( B
)
A.40 B.42 C.43 D.45
6. 把曲线ycosx+2y-1=0先沿x轴向右平移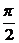 个单位,再沿y轴向下平移1个单位,得到的曲线方程是
(C)
个单位,再沿y轴向下平移1个单位,得到的曲线方程是
(C)
A.(1-y)sinx+2y-3=0 B.(y-1)sinx+2y-3=0
C.(y+1)sinx+2y+1=0 D.-(y+1)sinx+2y+1=0
7.从5位男教师和4位女教师中选出3位教师派到3个班担任班主任(每班1位班主任),要求这3位班主任中男女教师都有,则不同的选派方案共有( B )
A.210种 B.420种 C. 630种 D.840种
8. 若不等式组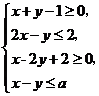 表示的平面区域是一个三角形,则
表示的平面区域是一个三角形,则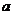 的取值范围是(D )
的取值范围是(D )
A.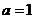 B.
B.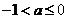 C.
C.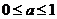 D.
D.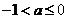 或
或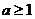
二、填空题。本大题共7个小题,每小题5分,共35分。把答案填在横线上。
9. 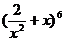 的展开式中的常数项是______60________(用数字作答).
的展开式中的常数项是______60________(用数字作答).
10.函数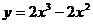 在区间[-1,2]上的最大值是__8________.
在区间[-1,2]上的最大值是__8________.
11. 球面上有3个点,其中任意两点的球面距离都等于大圆周长的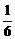 ,经过这3个点的小圆的周长为4π,那么这个球的半径为_____
,经过这3个点的小圆的周长为4π,那么这个球的半径为_____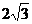 _______.
_______.
12. 过双曲线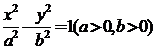 的左焦点,且垂直于
的左焦点,且垂直于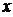 轴的直线与双曲线相交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于
2 .
轴的直线与双曲线相交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于
2 .
13. 把容量为100的某个样本数据分为10组,并填写频率分布表,若前七组的累积频率为0.79,而剩下三组的频数成公比大于2的整数等比数列,则剩下三组中频数最高的一组的频数为_______16____.
14. 点M在抛物线y2=ax上运动,点N与点M关于点A(1,1)对称,则点N的轨迹方程是 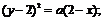 .
.
15. 给出下列函数:
①函数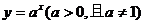 与函数
与函数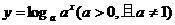 的定义域相同;
的定义域相同;
②函数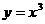 与
与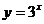 的值域相同;
的值域相同;
③函数y=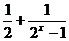 与
与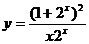 均是奇函数;
均是奇函数;
④函数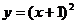 与
与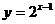 在
在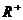 上都是增函数.
上都是增函数.
其中正确命题的序号是 ①③④ (把你认为正确的命题的序号都填上)
三、解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤。
16.在△ABC中,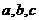 分别是
分别是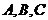 的对边,且
的对边,且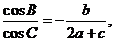
(1)求角B的大小;(2)若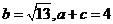 ,求
,求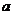 的值;
的值;
解:(1)由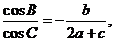 得
得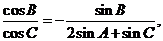
即: ∴
∴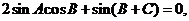
而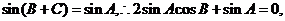 又
又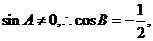
而
(2)利用余弦定理可解得: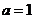 或
或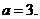




17.正三棱柱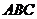 -
-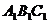 的底面边长为4,侧棱长为4,
的底面边长为4,侧棱长为4,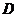 为
为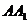 A1的中点,
A1的中点,

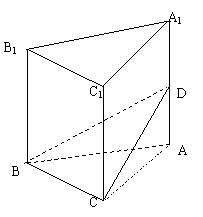 (1)求
(1)求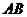 与
与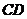 所成的角;(arccos
所成的角;(arccos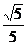 )
)
(2)求二面角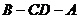 的大小;(arctan
的大小;(arctan )
)
(3)求点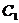 到平面BCD的距离。(2
到平面BCD的距离。(2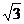 )
)

18.当下的金融危机使得年轻人开始重视多种技能的学习,某培训学校开设了计算机、英语、营销管理3门继续教育培训课程,若一共有100人报名,且3门课程分别有80、50、25人次参加(一人可参加多门课程,不同课程之间学习没有影响)。某记者随机采访了该校的2位学生。
(1)求至少有1人3门课程都参加了的概率。
(2)求3门课程中每一门恰有1人参加的概率。
解:由题意知:某人参加了这3门课程的概率分别为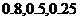 -----------------------(2分)
-----------------------(2分)
(1) 设事件Ai:第i个人3门课程都参加了(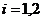 );
);
事件B:至少有1人3门课程都参加了。----------------------------------------(3分)
则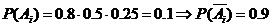 ,--------------------------------(4分)
,--------------------------------(4分)
Þ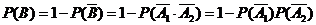 =
=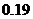 -----------------(6分)
-----------------(6分)
(2) 设事件Ci:第i门课程恰有1人参加(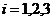 ),
),
事件D:3门课程中每一门都恰有1人参加.----------------------------------------(7分)
则: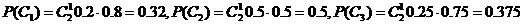
------------------------------------(10分)
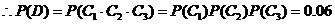 -----------------------------------(12分)
-----------------------------------(12分)
19.已知数列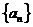 的前
的前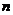 项和为
项和为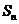 ,且
,且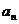 是
是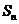 与2的等差中项,数列
与2的等差中项,数列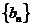 中,
中,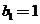 ,点
,点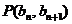 在直线
在直线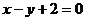 上。
上。
⑴求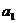 和
和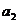 的值;
的值;
⑵求数列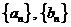 的通项
的通项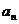 和
和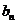 ;
;
⑶ 设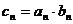 ,求数列
,求数列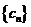 的前n项和
的前n项和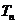 。
。
解:(1)∵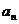 是
是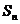 与2的等差中项,
与2的等差中项,
∴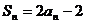 。
…………1分
。
…………1分
∴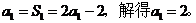
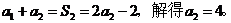 …………3分
…………3分
(2)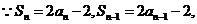
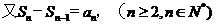
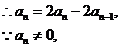 。
。
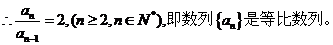
∵a1=2,∴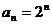 。
…………6分
。
…………6分
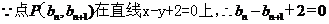 。
。
∴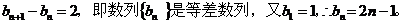 …………8分
…………8分
(3)
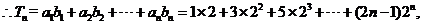 …………10分
…………10分
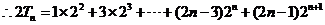 。
。
因此: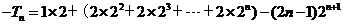 ,
12分
,
12分
即: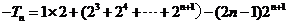 ,
,
∴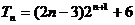 。
…………14分
。
…………14分
20设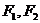 分别为椭圆
分别为椭圆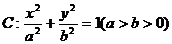 的左、右两个焦点,若椭圆C上的点
的左、右两个焦点,若椭圆C上的点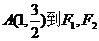 两点的距离之和等于4.
两点的距离之和等于4.
⑴ 求出椭圆C的方程和焦点坐标;
⑵ 过点P(0,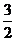 )的直线与椭圆交于两点M、N,若以M、N为直径的圆通过原点,求直线MN的方程.
)的直线与椭圆交于两点M、N,若以M、N为直径的圆通过原点,求直线MN的方程.
解:(Ⅰ)椭圆C的焦点在x轴上,
由椭圆上的点A到F1、F2两点的距离之和是4,得2a=4,即a=2.;
又点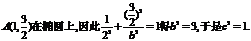 ;
;
所以椭圆C的方程为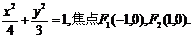 ,………6分
,………6分
(Ⅱ)直线MN不与x轴垂直,∴设直线MN方程为y=kx+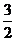 ,代入椭圆C的方程得
,代入椭圆C的方程得
(3+4k2)x2+12kx-3=0, 设M(x1,y1),N(x2,y2),则x1+x2=-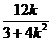 , x1x2=-
, x1x2=-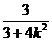 ,且△>0成立.
,且△>0成立.
又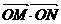 = x1x2+ y1y2= x1x2+( kx1+
= x1x2+ y1y2= x1x2+( kx1+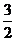 )(kx2+
)(kx2+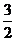 )=
-
)=
-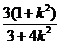 -
-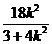 +
+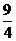 =0,
=0,
∴16k2=5,k=±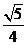 ,∴MN方程为y=±
,∴MN方程为y=±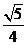 x+
x+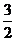 ……………14分
……………14分
20.对于三次函数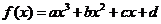
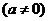 。
。
定义:(1)设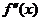 是函数
是函数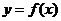 的导数
的导数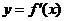 的导数,若方程
的导数,若方程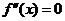 有实数解
有实数解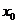 ,则称点
,则称点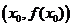 为函数
为函数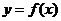 的“拐点”;
的“拐点”;
定义:(2)设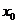 为常数,若定义在
为常数,若定义在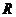 上的函数
上的函数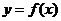 对于定义域内的一切实数
对于定义域内的一切实数 ,都有
,都有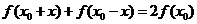 成立,则函数
成立,则函数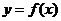 的图象关于点
的图象关于点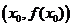 对称。
对称。
己知 ,请回答下列问题:
,请回答下列问题:
(1)求函数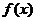 的“拐点”
的“拐点”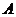 的坐标
的坐标
(2)检验函数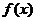 的图象是否关于“拐点”
的图象是否关于“拐点”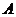 对称,对于任意的三次函数写出一个有关“拐点”的结论(不必证明)
对称,对于任意的三次函数写出一个有关“拐点”的结论(不必证明)
(3)写出一个三次函数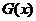 ,使得它的“拐点”是
,使得它的“拐点”是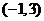 (不要过程)
(不要过程)
【标准答案】
(1)依题意,得: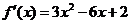 ,
,
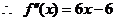 。……………………2分
。……………………2分
由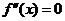 ,即
,即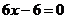 。∴
。∴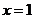 ,又
,又
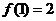 ,
,
∴ 的“拐点”坐标是
的“拐点”坐标是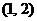 。……………………4分
。……………………4分
(2)由(1)知“拐点”坐标是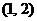 。
。
而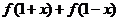 =
=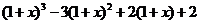
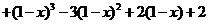
=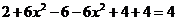 =
=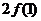 ,
,
由定义(2)知: 关于点
关于点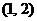 对称。……………………8分
对称。……………………8分
一般地,三次函数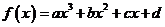
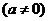 的“拐点”是
的“拐点”是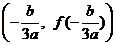 ,它就是
,它就是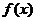 的对称中心。………………………………………………………………………10分
的对称中心。………………………………………………………………………10分
(或者:任何一个三次函数都有拐点;任何一个三次函数都有对称中心;任何一个三次函数平移后可以是奇函数………)都可以给分
(3)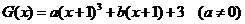 或写出一个具体的函数,如
或写出一个具体的函数,如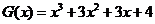 或
或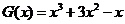 。…………12分
。…………12分