摘要:由定义(2)知:关于点对称.--------8分
网址:http://m.1010jiajiao.com/timu_id_534287[举报]
(本题满分18分)第(1)小题满分4分,第(2)小题满分8分,第(3)小题满分6分。
定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”。如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比。已知椭圆![]() 。
。
若椭圆![]() ,判断
,判断![]() 与
与![]() 是否相似?如果相似,求出
是否相似?如果相似,求出![]() 与
与![]() 的相似比;如果不相似,请说明理由;
的相似比;如果不相似,请说明理由;
 写出与椭圆
写出与椭圆![]() 相似且短半轴长为
相似且短半轴长为![]() 的椭圆
的椭圆![]() 的方程;若在椭圆
的方程;若在椭圆![]() 上存在两点
上存在两点![]() 、
、![]() 关于直线
关于直线![]() 对称,求实数
对称,求实数![]() 的取值范围?
的取值范围?
如图:直线![]() 与两个“相似椭圆”
与两个“相似椭圆”![]() 和
和![]() 分别交于点
分别交于点![]() 和点
和点![]() ,证明:
,证明:![]()
(本题满分18分)第(1)小题满分4分,第(2)小题满分8分,第(3)小题满分6分。
定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”。如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比。已知椭圆![]() 。
。
若椭圆![]() ,判断
,判断![]() 与
与![]() 是否相似?如果相似,求出
是否相似?如果相似,求出![]() 与
与![]() 的相似比;如果不相似,请说明理由;
的相似比;如果不相似,请说明理由;
 写出与椭圆
写出与椭圆![]() 相似且短半轴长为
相似且短半轴长为![]() 的椭圆
的椭圆![]() 的方程;若在椭圆
的方程;若在椭圆![]() 上存在两点
上存在两点![]() 、
、![]() 关于直线
关于直线![]() 对称,求实数
对称,求实数![]() 的取值范围?
的取值范围?
如图:直线![]() 与两个“相似椭圆”
与两个“相似椭圆”![]() 和
和![]() 分别交于点
分别交于点![]() 和点
和点![]() ,证明:
,证明:![]()
(本题满分18分,第(1)小题4分,第(2)小题6分,第(3)小题8分)
在平行四边形![]() 中,已知过点
中,已知过点![]() 的直线与线段
的直线与线段![]() 分别相交于点
分别相交于点![]() 。若
。若![]() 。
。
(1)求证:![]() 与
与![]() 的关系为
的关系为![]() ;
;
(2)设![]() ,定义函数
,定义函数![]() ,点列
,点列![]() 在函数
在函数![]() 的图像上,且数列
的图像上,且数列![]() 是以首项为1,公比为
是以首项为1,公比为![]() 的等比数列,
的等比数列,![]() 为原点,令
为原点,令![]() ,是否存在点
,是否存在点![]()
![]() ,使得
,使得![]() ?若存在,请求出
?若存在,请求出![]() 点坐标;若不存在,请说明理由。
点坐标;若不存在,请说明理由。
(3)设函数![]() 为
为![]() 上偶函数,当
上偶函数,当![]() 时
时![]() ,又函数
,又函数![]() 图象关于直线
图象关于直线![]() 对称, 当方程
对称, 当方程![]() 在
在![]() 上有两个不同的实数解时,求实数
上有两个不同的实数解时,求实数![]() 的取值范围。
的取值范围。
 中,已知过点
中,已知过点 的直线与线段
的直线与线段 分别相交于点
分别相交于点 。若
。若 。
。 与
与 的关系为
的关系为 ;
; ,定义函数
,定义函数 ,点列
,点列 在函数
在函数 的图像上,且数列
的图像上,且数列 是以首项为1,公比为
是以首项为1,公比为 的等比数列,
的等比数列, 为原点,令
为原点,令 ,是否存在点
,是否存在点
 ,使得
,使得 ?若存在,请求出
?若存在,请求出 点坐标;若不存在,请说明理由。
点坐标;若不存在,请说明理由。 为
为 上偶函数,当
上偶函数,当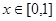 时
时 ,又函数
,又函数 对称, 当方程
对称, 当方程 在
在 上有两个不同的实数解时,求实数
上有两个不同的实数解时,求实数 的取值范围。
的取值范围。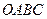 中,已知过点
中,已知过点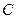 的直线与线段
的直线与线段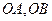 分别相交于点
分别相交于点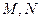 。若
。若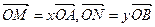 。
。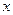 与
与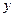 的关系为
的关系为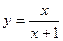 ;
;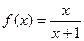 ,定义函数
,定义函数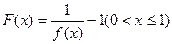 ,点列
,点列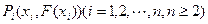 在函数
在函数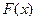 的图像上,且数列
的图像上,且数列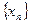 是以首项为1,公比为
是以首项为1,公比为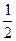 的等比数列,
的等比数列,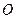 为原点,令
为原点,令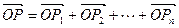 ,是否存在点
,是否存在点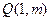
 ,使得
,使得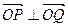 ?若存在,请求出
?若存在,请求出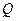 点坐标;若不存在,请说明理由。
点坐标;若不存在,请说明理由。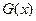 为
为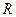 上偶函数,当
上偶函数,当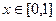 时
时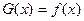 ,又函数
,又函数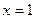 对称,当方程
对称,当方程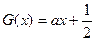 在
在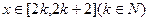 上有两个不同的实数解时,求实数
上有两个不同的实数解时,求实数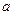 的取值范围。
的取值范围。