绝密★启用前
济宁市2008―2009学年度高三第一阶段质量检测
数学(文史类)试题2009.3
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.考试结束后,将本试卷和答题卡一并交回.
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用2B铅笔涂写在答题卡上.
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷上.
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共2小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.“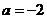 ”是“复数
”是“复数 为纯虚数”的
为纯虚数”的
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分又非必要条件
【解析】复数 为纯虚数”时,
为纯虚数”时,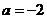 或
或 ,选A。
,选A。
2.给出命题:“若 ,则
,则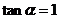 ”.在它的逆命题、否命题、逆否命题这三个命题中,真命题个数是
”.在它的逆命题、否命题、逆否命题这三个命题中,真命题个数是
A.3 B.2 C.1 D.0
【解析】若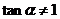 ,则
,则 ,显然逆命题、否命题不正确,选C。
,显然逆命题、否命题不正确,选C。
3.已知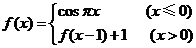 ,则
,则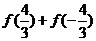 的值为
的值为
A.-2
B.-
【解析】 ,
,
所以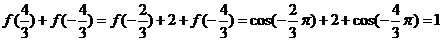 ,选C。
,选C。
4.若点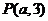 到直线
到直线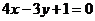 的距离为4,且点
的距离为4,且点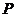 在不等式
在不等式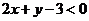 表示的平面区域内,则实数
表示的平面区域内,则实数 的值为
的值为
A.7 B.-7
C.3 D.-3
【解析】由若点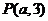 到直线
到直线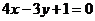 的距离
的距离
为4可得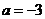 或
或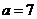 ;又点
;又点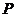 在不等式
在不等式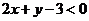 表示的平面区域内,所以
表示的平面区域内,所以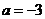 ,所以选D。
,所以选D。
 5.一个几何体的三视图如图所示,其中正视图与侧视图
5.一个几何体的三视图如图所示,其中正视图与侧视图
都是边长为2的正三角形,则这个几何体的侧面积为
A.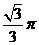 B.
B. 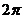
C.  D.
D. 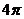
【解析】几何体为圆锥,侧面积为 ,
,
选B。
6.若关于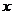 的不等式
的不等式 的解集是
的解集是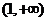 ,则关于
,则关于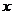 的不等式
的不等式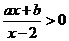 的解集是
的解集是
A. 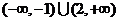 B.
B.  C.
C.  D.
D. 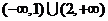
【解析】不等式 的解集是
的解集是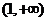 ,所以
,所以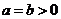 ,
,
所以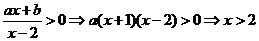 或
或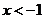 ,选A。
,选A。
总数和体重正常的频率分别为
 7.某校对高三年级的学生进行体检,现将高三男生的体重(单位:┧)数据进行整理后分为五组,并绘制频率分布直方图(如图所示).根据一般标准,高三男生的体重超过65┧属于偏胖,低于55┧属于偏瘦.已知图中从左到右第一、第三、第四、第五小组的频率分别为0.25、0.20、0.10、0.05,第二小组的频数为400,则该校高三年级的男生
7.某校对高三年级的学生进行体检,现将高三男生的体重(单位:┧)数据进行整理后分为五组,并绘制频率分布直方图(如图所示).根据一般标准,高三男生的体重超过65┧属于偏胖,低于55┧属于偏瘦.已知图中从左到右第一、第三、第四、第五小组的频率分别为0.25、0.20、0.10、0.05,第二小组的频数为400,则该校高三年级的男生
A.1000,0.50
B.800,0.50
C.800,0.60
D.1000,0.60
【解析】第二小组的频率为0.40,所以该校高三年级的男生
总数为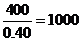 (人);体重正常的频率为0.40+0.20=0.60,选D。
(人);体重正常的频率为0.40+0.20=0.60,选D。
8.抛物线 的焦点坐标为
的焦点坐标为
A.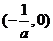 B.
B. C.
C. 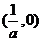 D.
D. 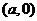
【解析】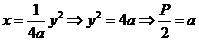 ,所以焦点坐标为
,所以焦点坐标为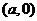 ,选D。
,选D。
9.在数列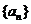 中,
中,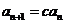 (
(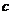 为非零常数),且前
为非零常数),且前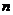 项和为
项和为 ,则实数
,则实数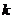 的值为
的值为
A.0 B.1 C.-1 D.2
【解析】 可得
可得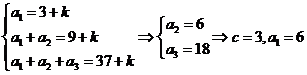 ,
,
所以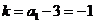 ,选C.
,选C.
10.已知向量 ,设
,设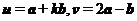 ,若
,若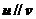 ,则实数
,则实数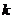 的值为
的值为
A.-1
B. C.
C. 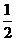 D. 1
D. 1
【解析】 ,选B.
,选B.
11.已知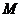 是
是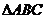 内的一点,且
内的一点,且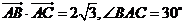 ,若
,若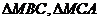 和
和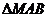 的面积分别为
的面积分别为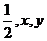 ,则
,则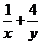 的最小值是
的最小值是
A.20 B.18 C.16 D.9
【解析】 ,
,
 ,选B.
,选B.
12.已知函数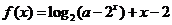 ,若
,若 存在零点,则实数
存在零点,则实数 的取值范围是
的取值范围是
A. B.
B.  C.
C. 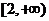 D.
D. 
【解析】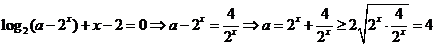 ,选D.
,选D.
第Ⅱ卷(非选择题 共90分)
注意事项:
1.第Ⅱ卷共2页,必须用0.5毫米的黑色墨水签字笔书写,作图时,可用2B铅笔.字体要工整,笔迹要清晰.严格在题号所指示的答题区域内作答.超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效.
2.答卷前将密封线内的项目填写清楚.
二、填空题:本大题共4小题,每小题4分,共16分.将答案填写在答题纸上.
13.已知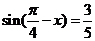 ,则
,则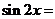 ▲
.
▲
.
【解析】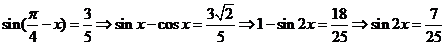 。
。
14.如果执行如图所示的程序,那么输出的值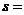 ▲ .
▲ .
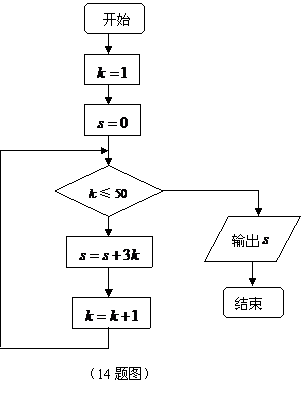 【解析】
【解析】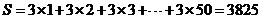 。
。
15.已知数列2008,2009,1,-2008,-2009,……这个数列的特点是从第二项起,每一项都等于它的前后两项之和,则这个数列的前2009项之和 等于
▲ .
等于
▲ .
【解析】略。
16.已知双曲线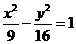 的左、右焦点分别为
的左、右焦点分别为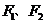 ,
,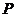 是双曲线上的一点,若
是双曲线上的一点,若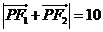 ,
,
则 ▲ .
▲ .
【解析】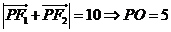 ,
,
在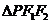 中
中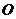 为
为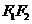 中点,
中点,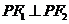 ,
,
所以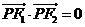 。
。
解答应写出文字说明、证明过程或演算步骤.
三、解答题:本大题共6个小题,共74分.
17.(本小题满分12分)
在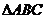 中,
中,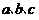 分别为角
分别为角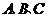 的对边,
的对边,
且满足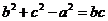 .
.
(Ⅰ)求角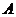 的值;
的值;
(Ⅱ)若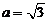 ,设角
,设角 的大小为
的大小为
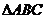 的周长为
的周长为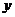 ,求
,求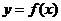 的最大值.
的最大值.
18. (本小题满分12分)
已知关于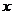 的一元二次方程
的一元二次方程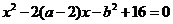 .
.
(Ⅰ)若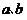 是一枚骰子掷两次所得到的点数,求方程有两正根的概率;
是一枚骰子掷两次所得到的点数,求方程有两正根的概率;
(Ⅱ)若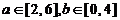 ,求方程没有实根的概率.
,求方程没有实根的概率.
 19. (本小题满分12分)
19. (本小题满分12分)
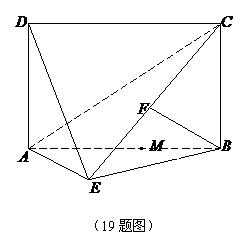
如图,四边形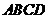 为矩形,
为矩形,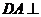 平面
平面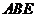 ,
,
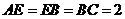 ,
, 平面
平面 于点
于点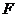 ,
,
且点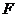 在
在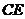 上.
上.
(Ⅰ)求证: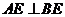 ;
;
(Ⅱ)求三棱锥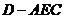 的体积;
的体积;
(Ⅲ)设点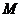 在线段
在线段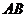 上,且满足
上,且满足 ,
,
试在线段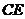 上确定一点
上确定一点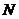 ,使得
,使得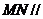 平面
平面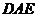 .
.
20. (本小题满分12分)
设同时满足条件:①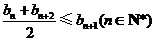 ;②
;②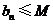 (
(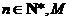 是与
是与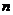 无关的常数)的无穷数列
无关的常数)的无穷数列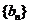 叫“特界” 数列.
叫“特界” 数列.
(Ⅰ)若数列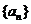 为等差数列,
为等差数列,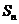 是其前
是其前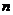 项和,
项和, ,求
,求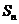 ;
;
(Ⅱ)判断(Ⅰ)中的数列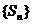 是否为“特界” 数列,并说明理由.
是否为“特界” 数列,并说明理由.
21. (本小题满分12分)
椭圆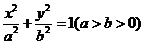 与直线
与直线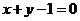 相交于
相交于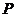 、
、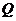 两点,且
两点,且 (
(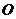 为坐标原点).
为坐标原点).
(Ⅰ)求证: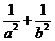 等于定值;
等于定值;
(Ⅱ)当椭圆的离心率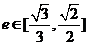 时,求椭圆长轴长的取值范围.
时,求椭圆长轴长的取值范围.
22.(本小题满分14分)
已知函数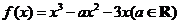 .
.
(Ⅰ)若函数 在区间
在区间 上为增函数,求实数
上为增函数,求实数 的取值范围;
的取值范围;
(Ⅱ)若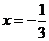 是函数
是函数 的极值点,求函数
的极值点,求函数 在区间
在区间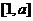 上的最大值;
上的最大值;
(Ⅲ)在(Ⅱ)的条件下,是否存在实数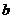 ,使得函数
,使得函数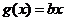 的图象与函数
的图象与函数 的图象恰有3个交点?若存在,请求出
的图象恰有3个交点?若存在,请求出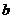 的取值范围;若不存在,试说明理由.
的取值范围;若不存在,试说明理由.
济宁市2008-2009学年度高三第一阶段质量检测
一、选择题(每小题5分,共60分)
1.A 2.C 3.C 4.D 5.B 6.A 7.D 8.D 9.C 10.B 11.B 12.D
二、填空题(每小题4分,共16分)
13. 14.3825 15.1 16.0ⅠⅡ
14.3825 15.1 16.0ⅠⅡ
三、解答题
17.解:(Ⅰ)在 中,由
中,由 及余弦定理得
及余弦定理得
而 ,则
,则 ;
;
(Ⅱ)由 及正弦定理得
及正弦定理得 ,
,
而 ,则
,则
于是 ,
,
由 得
得 ,当
,当 即
即 时,
时, 。
。
18解:(Ⅰ)基本事件 共有36个,方程有正根等价于
共有36个,方程有正根等价于 ,即
,即 。设“方程有两个正根”为事件
。设“方程有两个正根”为事件 ,则事件
,则事件 包含的基本事件为
包含的基本事件为 共4个,故所求的概率为
共4个,故所求的概率为 ;
;
(Ⅱ)试验的全部结果构成区域 ,其面积为
,其面积为
设“方程无实根”为事件 ,则构成事件
,则构成事件 的区域为
的区域为
 ,其面积为
,其面积为
故所求的概率为
19.解:(Ⅰ)证明:由 平面
平面 及
及 得
得 平面
平面 ,则
,则
而 平面
平面 ,则
,则 ,又
,又 ,则
,则 平面
平面 ,
,
又 平面
平面 ,故
,故 。
。
(Ⅱ)在 中,过点
中,过点 作
作 于点
于点 ,则
,则 平面
平面 .
.
由已知及(Ⅰ)得 .
.
故
(Ⅲ)在 中过点
中过点 作
作 交
交 于点
于点 ,在
,在 中过点
中过点 作
作 交
交 于点
于点 ,连接
,连接 ,则由
,则由 得
得
由平面 平面
平面 ,则
,则 平面
平面
再由 得
得 平面
平面 ,又
,又 平面
平面 ,则
,则 平面
平面 .
.
故当点 为线段
为线段 上靠近点
上靠近点 的一个三等分点时,
的一个三等分点时, 平面
平面 .
.
20.解:(Ⅰ)设等差数列 的公差为
的公差为 ,
,
则 ,
,
(Ⅱ)由
得 ,故数列
,故数列 适合条件①
适合条件①
而 ,则当
,则当 或
或 时,
时, 有最大值20
有最大值20
即 ,故数列
,故数列 适合条件②.
适合条件②.
综上,故数列 是“特界”数列。
是“特界”数列。
21. 证明:
证明: 消去
消去 得
得

设点 ,则
,则 ,
,
由 ,
, ,即
,即
化简得 ,则
,则
即 ,故
,故
(Ⅱ)解:由
化简得
由 得
得 ,即
,即
故椭圆的长轴长的取值范围是 。
。
22.解:(Ⅰ) ,由
,由 在区间
在区间 上是增函数
上是增函数
则当 时,恒有
时,恒有 ,
,
即 在区间
在区间 上恒成立。
上恒成立。
由 且
且 ,解得
,解得 .
.
(Ⅱ)依题意得
则 ,解得
,解得
而
故 在区间
在区间 上的最大值是
上的最大值是 。
。
(Ⅲ)若函数 的图象与函数
的图象与函数 的图象恰有3个不同的交点,
的图象恰有3个不同的交点,
即方程 恰有3个不等的实数根。
恰有3个不等的实数根。
而 是方程
是方程 的一个实数根,则
的一个实数根,则
方程 有两个非零实数根,
有两个非零实数根,
则 即
即 且
且 .
.
故满足条件的 存在,其取值范围是
存在,其取值范围是 .
.