网址:http://m.1010jiajiao.com/timu_id_491298[举报]
一、选择题(每小题5分,共60分)
1.A 2.C 3.C 4.D 5.B 6.A 7.D 8.D 9.C 10.B 11.B 12.D
二、填空题(每小题4分,共16分)
13. 14.3825 15.1 16.0ⅠⅡ
14.3825 15.1 16.0ⅠⅡ
三、解答题
17.解:(Ⅰ)在 中,由
中,由 及余弦定理得
及余弦定理得
而 ,则
,则 ;
;
(Ⅱ)由 及正弦定理得
及正弦定理得 ,
,
而 ,则
,则
于是 ,
,
由 得
得 ,当
,当 即
即 时,
时, 。
。
18解:(Ⅰ)基本事件 共有36个,方程有正根等价于
共有36个,方程有正根等价于 ,即
,即 。设“方程有两个正根”为事件
。设“方程有两个正根”为事件 ,则事件
,则事件 包含的基本事件为
包含的基本事件为 共4个,故所求的概率为
共4个,故所求的概率为 ;
;
(Ⅱ)试验的全部结果构成区域 ,其面积为
,其面积为
设“方程无实根”为事件 ,则构成事件
,则构成事件 的区域为
的区域为
 ,其面积为
,其面积为
故所求的概率为
19.解:(Ⅰ)证明:由 平面
平面 及
及 得
得 平面
平面 ,则
,则
而 平面
平面 ,则
,则 ,又
,又 ,则
,则 平面
平面 ,
,
又 平面
平面 ,故
,故 。
。
(Ⅱ)在 中,过点
中,过点 作
作 于点
于点 ,则
,则 平面
平面 .
.
由已知及(Ⅰ)得 .
.
故
(Ⅲ)在 中过点
中过点 作
作 交
交 于点
于点 ,在
,在 中过点
中过点 作
作 交
交 于点
于点 ,连接
,连接 ,则由
,则由 得
得
由平面 平面
平面 ,则
,则 平面
平面
再由 得
得 平面
平面 ,又
,又 平面
平面 ,则
,则 平面
平面 .
.
故当点 为线段
为线段 上靠近点
上靠近点 的一个三等分点时,
的一个三等分点时, 平面
平面 .
.
20.解:(Ⅰ)设等差数列 的公差为
的公差为 ,
,
则 ,
,
(Ⅱ)由
得 ,故数列
,故数列 适合条件①
适合条件①
而 ,则当
,则当 或
或 时,
时, 有最大值20
有最大值20
即 ,故数列
,故数列 适合条件②.
适合条件②.
综上,故数列 是“特界”数列。
是“特界”数列。
21. 证明:
证明: 消去
消去 得
得

设点 ,则
,则 ,
,
由 ,
, ,即
,即
化简得 ,则
,则
即 ,故
,故
(Ⅱ)解:由
化简得
由 得
得 ,即
,即
故椭圆的长轴长的取值范围是 。
。
22.解:(Ⅰ) ,由
,由 在区间
在区间 上是增函数
上是增函数
则当 时,恒有
时,恒有 ,
,
即 在区间
在区间 上恒成立。
上恒成立。
由 且
且 ,解得
,解得 .
.
(Ⅱ)依题意得
则 ,解得
,解得
而
故 在区间
在区间 上的最大值是
上的最大值是 。
。
(Ⅲ)若函数 的图象与函数
的图象与函数 的图象恰有3个不同的交点,
的图象恰有3个不同的交点,
即方程 恰有3个不等的实数根。
恰有3个不等的实数根。
而 是方程
是方程 的一个实数根,则
的一个实数根,则
方程 有两个非零实数根,
有两个非零实数根,
则 即
即 且
且 .
.
故满足条件的 存在,其取值范围是
存在,其取值范围是 .
.
(1)已知{an}是首项为2,公差为1的等差数列,若f(x)=kx,(k>1)是数列{an}的“保三角形函数”,求k的取值范围;
(2)已知数列{cn}的首项为2010,Sn是数列{cn}的前n项和,且满足4Sn+1-3Sn=8040,证明{cn}是“三角形”数列;
(3)[文科]若g(x)=lgx是(2)中数列{cn}的“保三角形函数”,问数列{cn}最多有多少项.
[理科]根据“保三角形函数”的定义,对函数h(x)=-x2+2x,x∈[1,A],和数列1,1+d,1+2d,(d>0)提出一个正确的命题,并说明理由. 查看习题详情和答案>>
(1)已知{an}是首项为2,公差为1的等差数列,若f(x)=kx,(k>1)是数列{an}的“保三角形函数”,求k的取值范围;
(2)已知数列{cn}的首项为2010,Sn是数列{cn}的前n项和,且满足4Sn+1-3Sn=8040,证明{cn}是“三角形”数列;
(3)根据“保三角形函数”的定义,对函数h(x)=-x2+2x,x∈[1,A],和数列1,1+d,1+2d(d>0)提出一个正确的命题,并说明理由.
(09年宜昌一中12月月考文)(12分)已知![]() 是定义在
是定义在![]() 上的函数,且满足下列条件:
上的函数,且满足下列条件:
① 对任意的![]() 、
、![]() ,
,![]() ;
;
② 当![]() 时,
时,![]() .
.
(1)证明![]() 在
在![]() 上是减函数;
上是减函数;
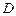 的函数
的函数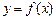 ,若有常数M,使得对任意的
,若有常数M,使得对任意的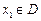 ,存在唯一的
,存在唯一的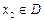 满足等式
满足等式 ,则称M为函数
,则称M为函数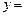 f (x)的“均值”.
f (x)的“均值”.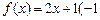 ≤
≤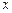 ≤
≤ 的“均值”,请说明理由;
的“均值”,请说明理由;
 为常数)存在“均值”,求实数a的取值范围;
为常数)存在“均值”,求实数a的取值范围; 是单调函数,且其值域为区间I.试探究函数
是单调函数,且其值域为区间I.试探究函数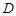 的函数
的函数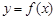 ,若有常数M,使得对任意的
,若有常数M,使得对任意的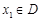 ,存在唯一的
,存在唯一的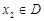 满足等式
满足等式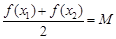 ,则称M为函数
,则称M为函数 f (x)的“均值”.
f (x)的“均值”. ≤
≤ ≤
≤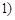 的“均值”,请说明理由;
的“均值”,请说明理由;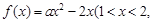
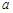 为常数)存在“均值”,求实数a的取值范围;
为常数)存在“均值”,求实数a的取值范围; 是单调函数,且其值域为区间I.试探究函数
是单调函数,且其值域为区间I.试探究函数