网址:http://m.1010jiajiao.com/timu_id_491249[举报]
一、选择题(每小题5分,共60分)
1.A 2.C 3.C 4.D 5.B 6.A 7.D 8.D 9.C 10.B 11.B 12.D
二、填空题(每小题4分,共16分)
13. 14.3825 15.1 16.0ⅠⅡ
14.3825 15.1 16.0ⅠⅡ
三、解答题
17.解:(Ⅰ)在 中,由
中,由 及余弦定理得
及余弦定理得
而 ,则
,则 ;
;
(Ⅱ)由 及正弦定理得
及正弦定理得 ,
,
而 ,则
,则
于是 ,
,
由 得
得 ,当
,当 即
即 时,
时, 。
。
18解:(Ⅰ)基本事件 共有36个,方程有正根等价于
共有36个,方程有正根等价于 ,即
,即 。设“方程有两个正根”为事件
。设“方程有两个正根”为事件 ,则事件
,则事件 包含的基本事件为
包含的基本事件为 共4个,故所求的概率为
共4个,故所求的概率为 ;
;
(Ⅱ)试验的全部结果构成区域 ,其面积为
,其面积为
设“方程无实根”为事件 ,则构成事件
,则构成事件 的区域为
的区域为
 ,其面积为
,其面积为
故所求的概率为
19.解:(Ⅰ)证明:由 平面
平面 及
及 得
得 平面
平面 ,则
,则
而 平面
平面 ,则
,则 ,又
,又 ,则
,则 平面
平面 ,
,
又 平面
平面 ,故
,故 。
。
(Ⅱ)在 中,过点
中,过点 作
作 于点
于点 ,则
,则 平面
平面 .
.
由已知及(Ⅰ)得 .
.
故
(Ⅲ)在 中过点
中过点 作
作 交
交 于点
于点 ,在
,在 中过点
中过点 作
作 交
交 于点
于点 ,连接
,连接 ,则由
,则由 得
得
由平面 平面
平面 ,则
,则 平面
平面
再由 得
得 平面
平面 ,又
,又 平面
平面 ,则
,则 平面
平面 .
.
故当点 为线段
为线段 上靠近点
上靠近点 的一个三等分点时,
的一个三等分点时, 平面
平面 .
.
20.解:(Ⅰ)设等差数列 的公差为
的公差为 ,
,
则 ,
,
(Ⅱ)由
得 ,故数列
,故数列 适合条件①
适合条件①
而 ,则当
,则当 或
或 时,
时, 有最大值20
有最大值20
即 ,故数列
,故数列 适合条件②.
适合条件②.
综上,故数列 是“特界”数列。
是“特界”数列。
21. 证明:
证明: 消去
消去 得
得

设点 ,则
,则 ,
,
由 ,
, ,即
,即
化简得 ,则
,则
即 ,故
,故
(Ⅱ)解:由
化简得
由 得
得 ,即
,即
故椭圆的长轴长的取值范围是 。
。
22.解:(Ⅰ) ,由
,由 在区间
在区间 上是增函数
上是增函数
则当 时,恒有
时,恒有 ,
,
即 在区间
在区间 上恒成立。
上恒成立。
由 且
且 ,解得
,解得 .
.
(Ⅱ)依题意得
则 ,解得
,解得
而
故 在区间
在区间 上的最大值是
上的最大值是 。
。
(Ⅲ)若函数 的图象与函数
的图象与函数 的图象恰有3个不同的交点,
的图象恰有3个不同的交点,
即方程 恰有3个不等的实数根。
恰有3个不等的实数根。
而 是方程
是方程 的一个实数根,则
的一个实数根,则
方程 有两个非零实数根,
有两个非零实数根,
则 即
即 且
且 .
.
故满足条件的 存在,其取值范围是
存在,其取值范围是 .
.
已知点 为圆
为圆 上的动点,且
上的动点,且 不在
不在 轴上,
轴上, 轴,垂足为
轴,垂足为 ,线段
,线段 中点
中点 的轨迹为曲线
的轨迹为曲线 ,过定点
,过定点
 任作一条与
任作一条与 轴不垂直的直线
轴不垂直的直线 ,它与曲线
,它与曲线 交于
交于 、
、 两点。
两点。
(I)求曲线 的方程;
的方程;
(II)试证明:在 轴上存在定点
轴上存在定点 ,使得
,使得 总能被
总能被 轴平分
轴平分
【解析】第一问中设 为曲线
为曲线 上的任意一点,则点
上的任意一点,则点 在圆
在圆 上,
上,
∴ ,曲线
,曲线 的方程为
的方程为
第二问中,设点 的坐标为
的坐标为 ,直线
,直线 的方程为
的方程为 , ………………3分
, ………………3分
代入曲线 的方程
的方程 ,可得
,可得 
∵ ,∴
,∴
确定结论直线 与曲线
与曲线 总有两个公共点.
总有两个公共点.
然后设点 ,
, 的坐标分别
的坐标分别 ,
,  ,则
,则 ,
,
要使 被
被 轴平分,只要
轴平分,只要 得到。
得到。
(1)设 为曲线
为曲线 上的任意一点,则点
上的任意一点,则点 在圆
在圆 上,
上,
∴ ,曲线
,曲线 的方程为
的方程为 . ………………2分
. ………………2分
(2)设点 的坐标为
的坐标为 ,直线
,直线 的方程为
的方程为 , ………………3分
, ………………3分
代入曲线 的方程
的方程 ,可得
,可得  ,……5分
,……5分
∵ ,∴
,∴ ,
,
∴直线 与曲线
与曲线 总有两个公共点.(也可根据点M在椭圆
总有两个公共点.(也可根据点M在椭圆 的内部得到此结论)
的内部得到此结论)
………………6分
设点 ,
, 的坐标分别
的坐标分别 ,
,  ,则
,则 ,
,
要使 被
被 轴平分,只要
轴平分,只要 ,
………………9分
,
………………9分
即 ,
, , ………………10分
, ………………10分
也就是 ,
, ,
,
即 ,即只要
,即只要 ………………12分
………………12分
当 时,(*)对任意的s都成立,从而
时,(*)对任意的s都成立,从而 总能被
总能被 轴平分.
轴平分.
所以在x轴上存在定点 ,使得
,使得 总能被
总能被 轴平分
轴平分
查看习题详情和答案>>
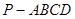 中,
中,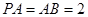 .
.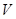 ;
;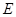 为侧棱
为侧棱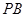 的中点,求异面直线
的中点,求异面直线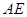 与
与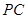
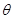 的大小.
的大小.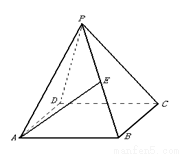
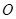 为底面正方形
为底面正方形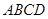 中心,则
中心,则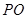 为该正四棱锥的高由已知,可求得
为该正四棱锥的高由已知,可求得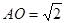 ,
,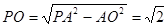
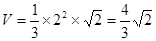
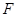 为
为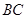 中点,连结
中点,连结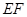 、
、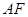 ,
,
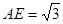 ,
,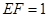 ,
,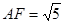 ,
,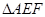 中,由余弦定理,得
中,由余弦定理,得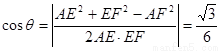 .
.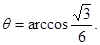
 ,则cos2α=
,则cos2α=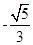 (B)
(B)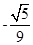 (C)
(C) 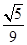 (D)
(D)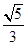
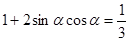 ,所以
,所以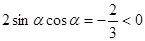 ,因为已知α为第二象限角,所以
,因为已知α为第二象限角,所以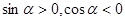 ,
,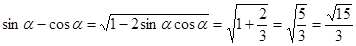 ,所以
,所以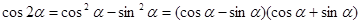 =
=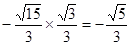 ,选A.
,选A. 的共轭复数是
的共轭复数是  ,所以其共轭复数为
,所以其共轭复数为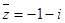 ,选D.
,选D.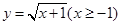 的反函数为
的反函数为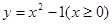 (B)
(B)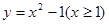
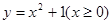 (D)
(D)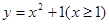
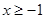 所以
所以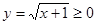 .由
.由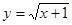 得,
得,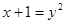 ,所以
,所以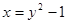 ,所以反函数为
,所以反函数为