网址:http://m.1010jiajiao.com/timu_id_491252[举报]
一、选择题(每小题5分,共60分)
1.A 2.C 3.C 4.D 5.B 6.A 7.D 8.D 9.C 10.B 11.B 12.D
二、填空题(每小题4分,共16分)
13. 14.3825 15.1 16.0ⅠⅡ
14.3825 15.1 16.0ⅠⅡ
三、解答题
17.解:(Ⅰ)在 中,由
中,由 及余弦定理得
及余弦定理得
而 ,则
,则 ;
;
(Ⅱ)由 及正弦定理得
及正弦定理得 ,
,
而 ,则
,则
于是 ,
,
由 得
得 ,当
,当 即
即 时,
时, 。
。
18解:(Ⅰ)基本事件 共有36个,方程有正根等价于
共有36个,方程有正根等价于 ,即
,即 。设“方程有两个正根”为事件
。设“方程有两个正根”为事件 ,则事件
,则事件 包含的基本事件为
包含的基本事件为 共4个,故所求的概率为
共4个,故所求的概率为 ;
;
(Ⅱ)试验的全部结果构成区域 ,其面积为
,其面积为
设“方程无实根”为事件 ,则构成事件
,则构成事件 的区域为
的区域为
 ,其面积为
,其面积为
故所求的概率为
19.解:(Ⅰ)证明:由 平面
平面 及
及 得
得 平面
平面 ,则
,则
而 平面
平面 ,则
,则 ,又
,又 ,则
,则 平面
平面 ,
,
又 平面
平面 ,故
,故 。
。
(Ⅱ)在 中,过点
中,过点 作
作 于点
于点 ,则
,则 平面
平面 .
.
由已知及(Ⅰ)得 .
.
故
(Ⅲ)在 中过点
中过点 作
作 交
交 于点
于点 ,在
,在 中过点
中过点 作
作 交
交 于点
于点 ,连接
,连接 ,则由
,则由 得
得
由平面 平面
平面 ,则
,则 平面
平面
再由 得
得 平面
平面 ,又
,又 平面
平面 ,则
,则 平面
平面 .
.
故当点 为线段
为线段 上靠近点
上靠近点 的一个三等分点时,
的一个三等分点时, 平面
平面 .
.
20.解:(Ⅰ)设等差数列 的公差为
的公差为 ,
,
则 ,
,
(Ⅱ)由
得 ,故数列
,故数列 适合条件①
适合条件①
而 ,则当
,则当 或
或 时,
时, 有最大值20
有最大值20
即 ,故数列
,故数列 适合条件②.
适合条件②.
综上,故数列 是“特界”数列。
是“特界”数列。
21. 证明:
证明: 消去
消去 得
得

设点 ,则
,则 ,
,
由 ,
, ,即
,即
化简得 ,则
,则
即 ,故
,故
(Ⅱ)解:由
化简得
由 得
得 ,即
,即
故椭圆的长轴长的取值范围是 。
。
22.解:(Ⅰ) ,由
,由 在区间
在区间 上是增函数
上是增函数
则当 时,恒有
时,恒有 ,
,
即 在区间
在区间 上恒成立。
上恒成立。
由 且
且 ,解得
,解得 .
.
(Ⅱ)依题意得
则 ,解得
,解得
而
故 在区间
在区间 上的最大值是
上的最大值是 。
。
(Ⅲ)若函数 的图象与函数
的图象与函数 的图象恰有3个不同的交点,
的图象恰有3个不同的交点,
即方程 恰有3个不等的实数根。
恰有3个不等的实数根。
而 是方程
是方程 的一个实数根,则
的一个实数根,则
方程 有两个非零实数根,
有两个非零实数根,
则 即
即 且
且 .
.
故满足条件的 存在,其取值范围是
存在,其取值范围是 .
.
 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)(1)已知曲线C的参数方程为
|
(2)已知不等式x+|x-2c|>1的解集为R,则正实数c的取值范围是
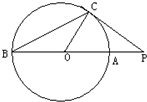
(3)如图,PC切圆O于点C,割线PAB经过圆心A,PC=4,PB=8,则S△OBC
 选考题
选考题请从下列三道题当中任选一题作答,如果多做,则按所做的第一题计分,请在答题卷上注明题号.
22-1设函数f(x)=|2x-1|+|2x-3|
(1)解不等式f(x)≤5x+1;
(2)若g(x)=
| 1 | ||
|
22-2如图,在△ABC中,CD是∠ACB的角平分线,△ACD的外接圆交BC于E,AB=2AC,
(1)求证:BE=2AD;
(2)当AC=1,BC=2时,求AD的长.
22-3已知P为半圆C:
|
| π |
| 3 |
(1)求以O为极点,x轴的正半轴为极轴建立极坐标系,求点M的极坐标;
(2)求直线AM的参数方程.
在极坐标系中,曲线C极坐标方程为ρ=2
| 2 |
| π |
| 4 |
|
求:(1)曲线C和直线l的普通方程;
(2)求直线l被曲线C所截得的弦长.
 知点
知点 是曲线
是曲线 上任意一点,则点
上任意一点,则点 的距离的最小值是 .
的距离的最小值是 . 的解集是 .
的解集是 . 和
和 分别是圆
分别是圆 的切线,且
的切线,且 ,
, ,延长
,延长 到
到 点,则
点,则 的面积是 .
的面积是 .