-
1. 已知映射
 ,其中
,其中 ,对应法则
,对应法则 若对实数
若对实数 ,在集合A中不存在原象,则
,在集合A中不存在原象,则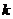 的取值范围是
( )
的取值范围是
( )A.
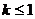 B.
B. C.
C.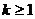 D.
D.
-
2.
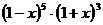 的展开式中
的展开式中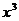 的系数为
( )
的系数为
( )A.
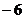 B.
B. C.
C. D.
D.
-
3.在等差数列
 中,若
中,若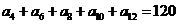 ,则
,则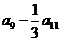 的值为
( )
的值为
( ) A.14 B.15 C.16 D.17
-
4.已知
 ,则
,则 的值为 (
)
的值为 (
) A.
 B.
B.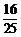 C.
C. D.
D.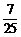
-
5.设地球的半径为
 ,若甲地位于北纬
,若甲地位于北纬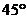 东经
东经 ,乙地位于南纬
,乙地位于南纬 东经
东经 ,则甲、乙两地的球面距离为
( )
,则甲、乙两地的球面距离为
( )A.
 B.
B.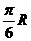 C.
C. D.
D.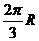
-
6.若
 是常数,则“
是常数,则“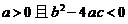 ”是“对任意
”是“对任意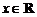 ,有
,有 ”的
( )
”的
( ) A.充分不必要条件. B.必要不充分条件.
C.充要条件. D.既不充分也不必要条件.
-
7.双曲线
 的左、右顶点分别为
的左、右顶点分别为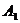 、
、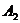 ,
, 为其右支上一点,且
为其右支上一点,且 ,则
,则 等于
( )
等于
( )A. 无法确定 B.
 C.
C. D.
D.
-
8.已知直线
 (
( 不全为
不全为 )与圆
)与圆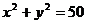 有公共点,且公共点的横、纵坐标均为整数,那么这样的直线有
( )
有公共点,且公共点的横、纵坐标均为整数,那么这样的直线有
( ) A.66条 B.72条
A.66条 B.72条
C.74条 D.78条
-
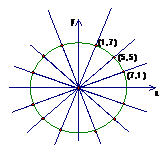
9.为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如右,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数为b,则a, b的值分别为( )
A.0,27,78 B.0,27,83
C.2.7,78 D.2.7,83
-
10.半径为4的球面上有A、B、C、D四点,且AB,AC,AD两两互相垂直,则
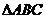 、
、 、
、 面积之和
面积之和 的最大值为 ( )
的最大值为 ( )A.8 B.16 C.32 D.64
-
11命题“若
 都是偶数,则
都是偶数,则 是偶数”的否命题是_________
是偶数”的否命题是_________
12. 以
 、
、 为焦点且过点
为焦点且过点 的双曲线的标准方程为 .
的双曲线的标准方程为 . -
13.定义一种运算“
 ”对于正整数满足以下运算性质:
”对于正整数满足以下运算性质:(1)
 ;(2)
;(2)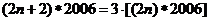 ,则
,则 的值是
的值是
-
14.
 的值等于
.
的值等于
. -
15.在△ABC中,角A,B,C所对的边分别是a,b,c,且
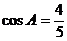 ,
,  ,△ABC的面积
,△ABC的面积 ,则a =
.
,则a =
. -
16.等比数列
 的公比为
的公比为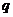 ,其前
,其前 项的积为
项的积为 ,并且满足条件
,并且满足条件 ,
, ,
, 。给出下列结论:①
。给出下列结论:①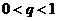 ;②
;② ③
③ 的值是
的值是  中最大的;④使
中最大的;④使 成立的最大自然数
成立的最大自然数 等于198。其中正确的结论是
.
等于198。其中正确的结论是
. -
17.(本小题满分12)已知向量
 .
.(1)向量
 是否共线?证明你的结论;
是否共线?证明你的结论;(2)若函数
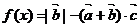 ,求
,求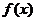 的最小值,并指出取得最小值时的
的最小值,并指出取得最小值时的 值.
值. -
18.(本小题满分14分)已知函数
 .
.(1)求
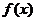 的定义域,并判断
的定义域,并判断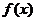 的奇偶性;
的奇偶性;(2)解关于
 的不等式:
的不等式: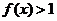 ;
; -
19.(本小题满分14分,第一、第二小问满分各6分)
如图,在斜三棱柱ABC-A1B1C1 中,侧面AA1B1B⊥底面ABC,侧棱AA1与底面ABC成600的角, AA1= 2.底面ABC是边长为2的正三角形,其重心为G点。E是线段BC1上一点,且BE=
 BC1 .
BC1 .(1)求证: GE∥侧面AA1B1B ;
 (2)求平面B1GE与底面ABC所成锐二面角的大小 .
(2)求平面B1GE与底面ABC所成锐二面角的大小 . -
20.(本小题满分14分)过抛物线
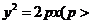

 的对称轴上的定点
的对称轴上的定点 ,作直线
,作直线 与抛物线相交于
与抛物线相交于 两点.
两点. (1)试证明
 两点的纵坐标之积为定值;
两点的纵坐标之积为定值; (2)若点
(2)若点 是定直线
是定直线 上的任一点,试探索三条直线
上的任一点,试探索三条直线 的斜率之间的关系,并给出证明.
的斜率之间的关系,并给出证明. -
21.(本小题满分14分)
已知
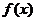 是二次函数,不等式
是二次函数,不等式 的解集是
的解集是 且
且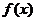 在区间
在区间 上的最大值是12。
上的最大值是12。(I)求
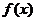 的解析式;
的解析式;(II)是否存在自然数
 使得方程
使得方程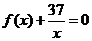 在区间
在区间 内有且只有两个不等的实数根?若存在,求出
内有且只有两个不等的实数根?若存在,求出 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。答案中学试卷网版权所有
-
1.B
提示:设
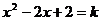 ,据题意知此方程应无实根
,据题意知此方程应无实根 ,
, 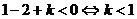 ,故选B
,故选B -
2. B
提示:


 展开式中
展开式中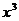 的系数为
的系数为 故选B
故选B -
3.C
提示:设等差数列
 的公差为
的公差为 , 由等差数列的性质知:
, 由等差数列的性质知:

 ,选C.
,选C. -
4.D
提示:由已知得
 ,两边平方得
,两边平方得 ,求得
,求得 .
.或令
 ,则
,则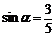 ,所以
,所以
-
5.D
提示:求两点间的球面距离,先要求出球心与这两点所成的圆心角的大小,∠AOB=120°,∴ A、B两点间的球面距离为
 ×2πR=
×2πR=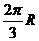 . 选D.
. 选D. -
6.A
提示:易知
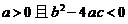

 对任意
对任意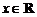 恒成立。
恒成立。反之,
 对任意
对任意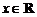 恒成立不能推出
恒成立不能推出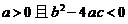
反例为当
 时也有
时也有 对任意
对任意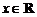 恒成立
恒成立“
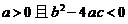 ”是“对任意
”是“对任意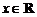 ,有
,有 的充分不必要条件,选A.
的充分不必要条件,选A. -
7.D
提示:设
 ,
, ,过点
,过点 作
作 轴的垂线
轴的垂线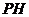 ,垂足为
,垂足为 ,则
,则
 ( 其中
( 其中 )
)



设
 , 则
, 则



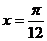 , 即
, 即 ,
故选 D.
,
故选 D. -
8.B
 提示:先考虑
提示:先考虑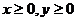 时,圆上横、纵坐标均为整数的点有
时,圆上横、纵坐标均为整数的点有 、
、 、
、 ,依圆的对称性知,圆上共有
,依圆的对称性知,圆上共有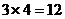 个点横纵坐标均为整数,经过其中任意两点的割线有
个点横纵坐标均为整数,经过其中任意两点的割线有 条,过每一点的切线共有12条,又考虑到直线
条,过每一点的切线共有12条,又考虑到直线 不经过原点,而上述直线中经过原点的有6条,所以满足题意的直线共有
不经过原点,而上述直线中经过原点的有6条,所以满足题意的直线共有 条,故选B.
条,故选B. -
9.
(理科做)A
提示:注意到纵轴表示
 ,
,由图象可知,前4组的公比为3,
最大频率
 ,设后六组公差为
,设后六组公差为 ,则
,则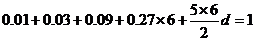 ,解得:
,解得: ,
,即后四组公差为
 , 所以,视力在4.6到5.0之间的学生数为
, 所以,视力在4.6到5.0之间的学生数为 -
0.27+0.22+0.17+0.12)×100=78(人).选A.
-
10.C
提示:由AB,AC,AD两两互相垂直,将之补成长方体知AB2+AC2+AD2=(2R)2=64.
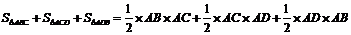
≤
 =
= .
.等号当且仅当
 取得,所以
取得,所以 的最大值为32 ,选C.
的最大值为32 ,选C. -
11. 若
 不都是偶数,则
不都是偶数,则 不是偶数
12.
不是偶数
12.
-
13.
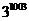 提示:设
提示:设 则
则 且
且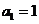

 , 即
, 即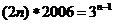 ,
,
-
14.
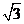 15.
15. 16. ①②④
16. ①②④ -
17.
解:(1)因为
 ,
,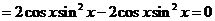
所以
 . ……… 6分
. ……… 6分
(2)


 …………10分
…………10分 因为
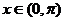 ,
所以
,
所以
则
 ,即
,即 时,
时,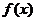 取得最小值
取得最小值 ………13分
………13分 -
18.解:(1)
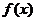 定义域为
定义域为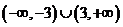 关于原点对称,
关于原点对称,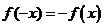 为奇函数;
为奇函数;(2)当
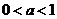 时,
时,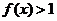




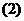

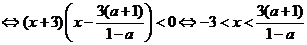
原不等式解集:

当
 时,
时,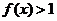

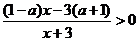

原不等式解集:
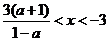
-
19. 解:(1)延长B1E交BC于F, ∵ΔB1EC∽ΔFEB, BE=
 EC1
EC1∴BF=
 B1C1=
B1C1= BC,从而F为BC的中点.
BC,从而F为BC的中点. ∵G为ΔABC的重心,∴A、G、F三点共线,且
 =
=  =
= ,∴GE∥AB1,
,∴GE∥AB1,又GE
 侧面AA1B1B,
∴GE∥侧面AA1B1B
侧面AA1B1B,
∴GE∥侧面AA1B1B (2)在侧面AA1B1B内,过B1作B1H⊥AB,垂足为H,∵侧面AA1B1B⊥底面ABC,
∴B1H⊥底面ABC.又侧棱AA1与底面ABC成600的角, AA1= 2,
∴∠B1BH=600,BH=1,B1H=
 .
.在底面ABC内,过H作HT⊥AF,垂足为T,连B1T.由三垂线定理有B1T⊥AF,
又平面B1GE与底面ABC的交线为AF,∴∠B1TH为所求二面角的平面角.
∴AH=AB+BH=3,∠HAT=300, ∴HT=AHsin300=
 ,
,在RtΔB1HT中,tan∠B1TH=
 =
=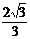 ,
,从而平面B1GE与底面ABC所成锐二面角的大小为arctan
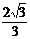
-
20.(1)证明:.设
 有
有 ,下证之:
,下证之:设直线
 的方程为:
的方程为: 与
与 联立得
联立得


消去
 得
得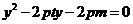
由韦达定理得

 ,
,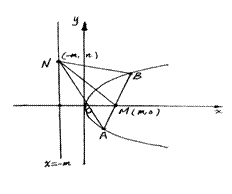 (2)解:三条直线
(2)解:三条直线 的斜率成等差数列,下证之:
的斜率成等差数列,下证之:设点
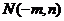 ,则直线
,则直线 的斜率为
的斜率为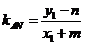 ;
;直线
 的斜率为
的斜率为




又
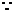 直线
直线 的斜率为
的斜率为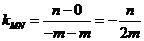
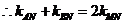
即直线
 的斜率成等差数列.
的斜率成等差数列.21题:(I)解:
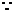
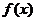 是二次函数,且
是二次函数,且 的解集是
的解集是
 可设
可设
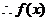 在区间
在区间 上的最大值是
上的最大值是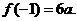
由已知,得


(II)方程
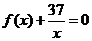 等价于方程
等价于方程
设
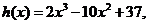 则
则
当
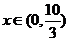 时,
时, 是减函数;当
是减函数;当 时,
时,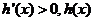 是增函数。
是增函数。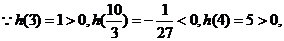
 方程
方程 在区间
在区间 内分别有惟一实数根,而在区间
内分别有惟一实数根,而在区间
 内没有实数根,
内没有实数根,所以存在惟一的自然数
 使得方程
使得方程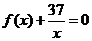 在区间
在区间 内有且只有两个不同的实数根。
内有且只有两个不同的实数根。