-
网址:http://m.1010jiajiao.com/paper/timu/5155786.html[举报]
17.
解:(1)因为
 ,
,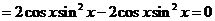
所以
 . ……… 6分
. ……… 6分
(2)


 …………10分
…………10分 因为
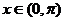 ,
所以
,
所以
则
 ,即
,即 时,
时,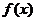 取得最小值
取得最小值 ………13分
………13分 - 题目来源:高三数学综合练习(23)
网址:http://m.1010jiajiao.com/paper/timu/5155786.html[举报]
17.
解:(1)因为 ,
,
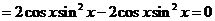
所以 . ……… 6分
. ……… 6分
(2)

 …………10分
…………10分
因为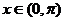 ,
所以
,
所以
则 ,即
,即 时,
时,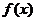 取得最小值
取得最小值 ………13分
………13分