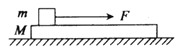
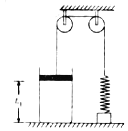
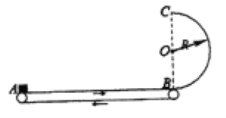
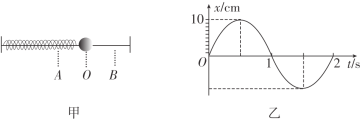0 176239 176247 176253 176257 176263 176265 176269 176275 176277 176283 176289 176293 176295 176299 176305 176307 176313 176317 176319 176323 176325 176329 176331 176333 176334 176335 176337 176338 176339 176341 176343 176347 176349 176353 176355 176359 176365 176367 176373 176377 176379 176383 176389 176395 176397 176403 176407 176409 176415 176419 176425 176433 176998