��Ŀ����
����Ŀ����ͼ��ʾ���ס��������ʹ���ˮƽ��ļн���ͬ�����Ժ㶨����v�����˶����ֽ�һ����Ϊm��С���壨��Ϊ�ʵ㣩�������A����С�����ڼ״��ʹ��ϵ���B��ʱǡ�ôﵽ���ʹ�������v�����Ҵ��ʹ��ϵ�����B����ֱ�߶�Ϊh��C��ʱ�ﵽ���ʹ�������v����֪B�������ĸ߶Ⱦ�ΪH������С�����A��B�Ĺ����У�������
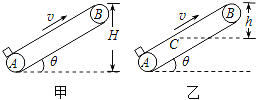
A. С������״��ʹ���Ķ�Ħ��������С
B. �����ʹ���С�����������
C. �����ʹ����ĵĵ������
D. �����������Ħ���������������
���𰸡�AB
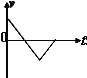
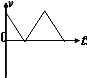
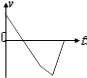
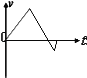
�����������ݹ�ʽv2=2ax����֪������ٶȹ�ϵa����a��������ţ�ٵڶ����ɦ�mgcos��-mgsin��=ma����֪��������������A��ȷ�����ʹ���С������������С���Ļ�е�ܵ���������������������ȣ��������ܵ�������Ҳ��ͬ�������ִ��ʹ���С����������ȣ���B��ȷ����Ħ������Q=fS���֪����ͼ�У� ![]() ��
�� ![]() ��
�� 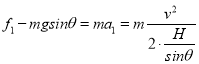
��ͼ�У� ![]() ��
�� 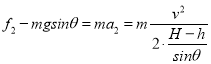
��ã�Q��=mgH+![]() mv2��Q��=mg��H-h��+
mv2��Q��=mg��H-h��+![]() mv2��Q����Q������D����
mv2��Q����Q������D����
���������غ㶨�ɣ��綯�����ĵĵ���E������Ħ������������Q��������ӻ�е��֮�ͣ���������δ�A��B���ӵĻ�е����ͬ��Q����Q�������Խ�С���崫�͵�B�������ִ��ʹ����ĵĵ��ܼ��࣬��C����ѡAB��

 ϰ�⾫ѡϵ�д�
ϰ�⾫ѡϵ�д�