题目内容
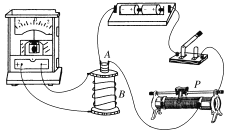
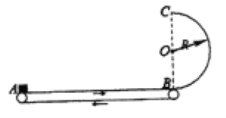
【题目】如图所示,水平传送带上A、B两端点间距L=4m,半径R=1m的光滑半圆形轨道固于竖直平面内,下端与传送带B相切。传送带以v0=4m/s的速度沿图示方向匀速运动,质量m=lkg的小滑块由静止放到传送带的A端,经一段时间运动到B端,滑块与传送带间的动摩擦因数μ=0.5,取g=10m/s2。
(1)求滑块到达B端的速度;
(2)求滑块由A运动到B的过程中,滑块与传送带间摩擦产生的热量;
(3)仅改变传送带的速度,其他条件不变,计算说明滑块能否通过圆轨道最高点C。
【答案】(1)vB=4m/s (2)Q=8J (3)不能通过最高点
【解析】试题分析:⑴滑块开始时在传送带上先向右做加速运动,若传送带足够长,设当滑块速度v=v0时已运动距离为x,根据动能定理有:μmgx=![]() -0
-0
解得:x=1.6m<L, 所以滑块将以速度v=v0=4m/s做匀速运动至B端
⑵设滑块与传送带发生相对运动的时间为t,则:v0=μgt
皮带通过的位移为:x′=v0t
滑块与传送带之间相对滑动的距离为:Δx=x′-x
滑块与传送带之间产生的热量为:Q=μmgΔx
联立以上各式解得:Q=8J
⑶设滑块通过最高点C的最小速度为vC,经过C点时,根据向心力公式和牛顿第二定律有:mg=![]()
在滑块从B运动到C的过程中,根据动能定理有:-2mgR=![]() -
-![]()
解得要使滑块能通过圆轨道最高点C时经过B的速度最小为:vB=![]() m/s
m/s
若仅改变传送带的速度,其他条件不变,使得滑块一直做匀加速直线运动至B的速度为最大速度,设为vm,根据动能定理有:μmgL=![]() -0
-0
解得:vm=![]() m/s<vB=
m/s<vB=![]() m/s,所以仅改变传送带的速度,滑块不能通过圆轨道最高点
m/s,所以仅改变传送带的速度,滑块不能通过圆轨道最高点
考点:本题主要考查了匀变速直线运动规律、牛顿第二定律、动能定理、功能关系的应用问题,属于中档题。
【题型】解答题
【结束】
23
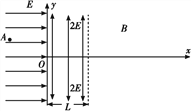
【题目】如图所示,在xOy平面内,y轴左侧有沿x轴正方向的匀强电场,电场强度大小为E;在0<x<L区域内,x轴上、下方有相反方向的匀强电场,电场强度大小均为2E;在x>L的区域内有垂直于xOy平面的匀强磁场,磁感应强度大小不变、方向做周期性变化.一电荷量为q、质量为m的带正电粒子(粒子重力不计),由坐标为(-L, ![]() )的A点静止释放.
)的A点静止释放.
(1)求粒子第一次通过y轴时速度的大小;
(2)求粒子第一次射入磁场时的位置坐标及速度;
(3)现控制磁场方向的变化周期和释放粒子的时刻,实现粒子能沿一定轨道做往复运动,求磁场的磁感应强度B的大小取值范围.
【答案】(1) ![]() (2)(L,L)
(2)(L,L) ![]() ,方向与x轴正方向成45°角斜向上 (3)
,方向与x轴正方向成45°角斜向上 (3) ![]()
【解析】试题分析:(1)对于粒子从A点到y轴的过程,运用动能定理求解粒子第一次通过y轴时速度大小;(2)进入0<x<L区域间偏转电场时作类平抛运动,由运动的分解法,求出偏转的距离,确定第一次射入磁场时的位置坐标.由速度的合成求出粒子第一次射入磁场时的速度.(3)在磁场中,粒子做匀速圆周运动,由洛伦兹力提供向心力,求出轨迹半径表达式.要实现粒子能沿一定轨道做往复运动,粒子的运动轨迹关于x轴必须对称,根据对称性和几何关系得到轨迹半径的最小值,求得B的最大值,从而求得磁场的磁感应强度B大小取值范围.
(1)粒子从A点到y轴的过程,根据动能定理得![]() ,得
,得![]() ;
;
(2)进入![]() 区域间偏转电场作类平抛运动,则得
区域间偏转电场作类平抛运动,则得![]() ,
, ![]() ,
, ![]()
解得![]()
所以第一次射入磁场时的位置坐标为(L,L);
速度大小![]() ,方向与x轴正方向成45°角斜向上.
,方向与x轴正方向成45°角斜向上.
(3)在磁场中,粒子做匀速圆周运动,根据向心力公式有![]()
轨道半径![]()
由对称性可知,射出磁场后必须在x轴下方的电场中运动,才能实现粒子沿一定轨道做往复运动,如图所示.

当![]() 时,轨道半径R最小,对应的磁感应强度B最大,粒子紧贴x轴进入y轴左侧的电场.
时,轨道半径R最小,对应的磁感应强度B最大,粒子紧贴x轴进入y轴左侧的电场.
由几何关系得![]() 得最小半径
得最小半径![]() ,
,
磁感应强度的最大值: ![]()
磁感应强度大小取值范围为![]()

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案