题目内容
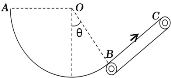
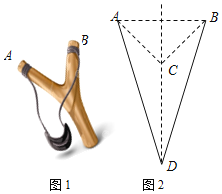
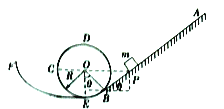
【题目】游乐场的过山车可以底朝上在圆轨道上送行，游客却不会掉下来。我们把这种情况抽象为如右图的模型。如图所示，AB是倾角为θ粗糙直轨道，BCD是光滑的圆环轨道，AB恰好在B点与圆弧相切，圆弧的半经为R，一个质量为m的物体（可以看做质成)从直轨道上的P点由静止释放，结果能在两轨道间做往返运动。已知P点与圆弧的圆心等高，物体与轨道AB间的动摩擦因数为μ。求：
（1）物体第一次到达B点时的速度大小；
（2）物体做往返运动的整个过程中在AB轨道上通过的总路程；
（3）为使物体能顺利到达圆轨道的最高点D，释放点距B点的距离
应满足什么条件?
【答案】（1）
（2）
（3）L′≥
【解析】
（1）设物体第一次到达B点的速度为vB，由动能定理可知
（mgsinθ-μmgcosθ）
=
mvB2-0
得
（2）物体在P点及最终到B点的速度都为零，对全过程由动能定理得
mgRcosθ-μmgcosθs=0
得s=R/μ
（3）设物体刚好通过D点时的速度为vD，有：mg=m
，
得：vD=
设物体恰好通过D点时释放点距B点的距离为L0，在粗糙直轨道上重力的功WG1=mgL0sinθ
滑动摩擦力的功：Wf=-μmgcosθL0
在光滑圆弧轨道上重力的功WG2=-mgR（1+cosθ）
对全过程由动能定理得WG1+WG2+Wf=mvD2-0
解得L0=
则L′≥
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
