题目内容
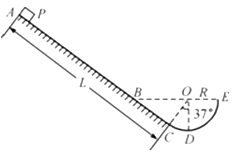
【题目】如图所示，斜面ABC下端与光滑的圆弧轨道CDE相切于C，整个装置竖直固定，D是最低点，圆心角∠DOC=37°，E、B与圆心O等高，圆弧轨道半径R=0.30m，斜面长L=1.90m，AB部分光滑，BC部分粗糙。现有一个质量m=0.10kg的小物块P从斜面上端A点无初速下滑，物块P与斜面BC部分之间的动摩擦因数μ=0.75。取sin37°=0.6，cos37°=0.8，重力加速度g=10m/s2，忽略空气阻力.求：
（1）物块通过B点时的速度大小vB；
（2）物块第一次通过C点时的速度大小vC；
（3）物块第一次通过D点后能上升的最大高度；
（4）分析说明物块最终处于什么状态。
【答案】(1) 
(2) 
(3) 0.96m (4) 物块最终将停在BC之间的某处
【解析】试题分析：根据几何关系求出BC部分的长度，对A到B运用动能定理，求出B点的速度，根据物体在粗糙斜面上的受力判断出物体做匀速直线运动，从而得出C点的速度；物块在光滑的CDE曲面内运动中，只有重力做功机械能守恒即可求出上升的最大高度；当物块速度逐渐减到零时，由于物块重力沿着斜面的分力Gx=0.6 N，而物块的摩擦力大小f=0.6N，受力平衡，可得出物块最终将停止在BC之间的某处。
（1）根据几何关系得，斜面BC部分的长度为： 
物块在AB段运动的过程中只有重力做功，
由机械能守恒定律得： 
解得：vB=4.24m/s
（2）物块在BC部分滑动受到的摩擦力大小为： 
物块重力沿着斜面分力
，所以在BC部分物块受到的合力为0，物体做匀速直线运动，所以物块第一次通过C点时的速度：vC=4.24m/s
（3）物块在光滑的CDE曲面内运动中，只有重力做功机械能守恒，取D处为零势能面，设物块最多上升高度为H，由机械能守恒定律得：
解得：H=0.96m
（4）物块从曲面返回后进入BC段，每通过一次BC段，都会损失机械能。当物块速度逐渐减到0时，由于物块重力沿着斜面的分力Gx=0.6 N，而物块的摩擦力大小f=0.6N，受力平衡，所以物块最终将停止在BC之间的某处。
