题目内容
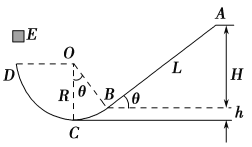
【题目】如图所示,粗糙的斜面AB下端与光滑的圆弧轨道BCD相切于B,整个装置竖直放置,C是最低点,圆心角θ=37°,D与圆心O等高,圆弧轨道半径R=1m,斜面长L=4m。现有一个质量m=0.1kg的小物体P从斜面AB上端A点无初速度下滑,物体P与斜面AB之间的动摩擦因数μ=0.25。不计空气阻力,g=10m/s2,sin37°=0.6,cos37°=0.8,求:
(1)物体P第一次通过B点时的速度大小v;
(2)物体P第一次通过C点时对轨道的压力大小FN;
(3)物体P从D点向上到达最高点为E,求E到D的高度。
【答案】(1)![]() ;(2)4.6N;(3)0.8m
;(2)4.6N;(3)0.8m
【解析】
(1)物体从A到B点过程,根据动能定理得
![]()
解得
![]()
(2)物体从A到C点过程,根据动能定理得
![]()
代入数据解得
![]()
在C点,由牛顿第二定律得
![]()
代入数据解得
![]()
由牛顿第三定律得:物体P第一次通过C点时对轨道的压力大小为4.6N。
(3)设D点到E点的高度为h,从C点到E点,由动能定理可得
![]()
解得
![]()

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目