题目内容
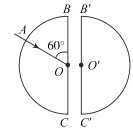
【题目】如图所示,两块半径均为R的半圆形玻璃砖正对放置,折射率均为n=![]() ;沿竖直方向的两条直径BC、B′C′相互平行,一束单色光正对圆心O从A点射入左侧半圆形玻璃砖,知∠AOB=60°。若不考虑光在各个界面的二次反射,下列说法正确的是( )
;沿竖直方向的两条直径BC、B′C′相互平行,一束单色光正对圆心O从A点射入左侧半圆形玻璃砖,知∠AOB=60°。若不考虑光在各个界面的二次反射,下列说法正确的是( )
A.减小∠AOB,光线可能在BC面发生全反射
B.BC、B′C′间距大小与光线能否从右半圆形玻璃砖右侧射出无关
C.如果BC、B′C′间距大于![]() ,光线不能从右半圆形玻璃砖右侧射出
,光线不能从右半圆形玻璃砖右侧射出
D.如果BC、B′C′间距等于![]() ,光线穿过两个半圆形玻璃砖的总偏折角为15°
,光线穿过两个半圆形玻璃砖的总偏折角为15°
【答案】AD
【解析】
A.玻璃砖的临界角为
![]()
解得
C=45°
所以减小∠AOB,光线可能在BC面发生全反射,故A正确;
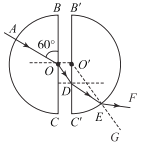
D.由折射定律可得∠O′OD=45°,则
OO′=O′D=![]() ,∠O′DE=120°
,∠O′DE=120°
在△O′DE中,由正弦定理可得

又
![]()
代入数据可得∠O′ED=30°,由折射定律可得∠FEG=45°,所以光线EF相对于光线AO偏折了15°,故D正确;
BC.BC、B′C′间距越大,从右半圆圆弧出射光线的入射角就越大,可能超过临界角,所以BC、B′C′间距大小与光线能否从右半圆形玻璃右侧射出有关,且当入射角小于45°时均可从右侧面射出,故BC错误。
故选BC。

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目