题目内容
【题目】汽车A以vA=4 m/s的速度向右做匀速直线运动,发现前方相距x0=7 m处、以vB=10 m/s的速度同向运动的汽车B正开始匀减速刹车直到静止后保持不动,其刹车的加速度大小a=2 m/s2.从此刻开始计时,求:
(1)A追上B前,A、B间的最远距离是多少?
(2)经过多长时间A恰好追上B?
【答案】(1)16 m (2)8 s
【解析】
汽车A和B运动的过程如图所示:
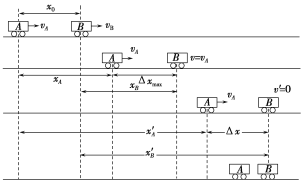
(1)当A、B两汽车速度相等时,两车间的距离最远,即
v=vB-at=vA,
解得t=3s
此时汽车A的位移
xA=xAt=12m
汽车B的位移
xB=vBt-![]() at2=21m
at2=21m
故最远距离
Δxmax=xB+x0-xA=16m.
(2)汽车B从开始减速直到静止经历的时间
![]()
运动的位移
![]()
汽车A在t1时间内运动的位移
![]()
此时相距
![]()
汽车A需再运动的时间
![]()
故A追上B所用时间
t=t1+t2=8s

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目