Question

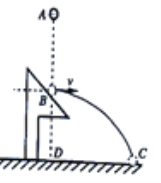
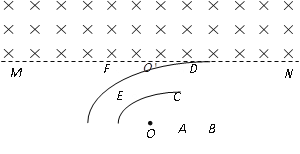
【题目】如图所示，在真空区域有半径不等的两个带电金属半圆球面A、B，点O为它们共同的球心，B球半径为R，两球面各自为电势不等的等势体，A球面的电势为φA，B球面的电势为φB，与B球面相切于点的直线边界线MN的另一侧充满了方向垂直于纸面向内磁感应强度为B0的匀强磁场．一质量为m，电荷量为q的正电粒子甲自O点以初速度v0沿半径方向发射，先后穿过金属球面上的小孔C、D，之后自P点（图中未画出）进入磁场．已知弧的弧度为．

（1）求粒子进入磁场时的速度大小．

（2）粒子从点（图中未画出）离开磁场，求点与点的间距及粒子从点运动至的时间．

（3）另一与粒子甲完全相同的粒子乙自O点以相同初速度v0沿半径方向发射，先后穿过金属球面上的小孔E、F，之后自点（图中未画出）进入磁场，从点（图中未画出）离开磁场，已知弧的弧度也为．计算点与点的间距，并判断当磁场的磁感应强度B0增加后，再次让两粒子完成上述运动，则点与点的间距将如何变化？

Answer 1

【答案】（1） （2）（3），不变

【解析】

(1)两球面间的电势差

设进入磁场经过P点时的速度为v1

从O点到进入磁场的P点，由动能定理的：

代入得：

(2)圆周运动

得：

由几何关系得：

代入得：

(3)圆周运动

得：

由几何关系得：

代入得：

故点与点的间距与磁场入射点P点和Q点的距离相同,即

当磁场的磁感应强度B0增加后，再次让两粒子完成上述运动，则点与点的间距不变．