��Ŀ����
����Ŀ����ͼ��ʾ���뾶ΪR���ķ�֮һ�⻬Բ�ι̶�����Ҷ�����һ�⻬��ˮƽ�棬����ΪM=3m��С��Q���������ʵ��ɾ�ֹ��ˮƽ���ϣ�����һ����Ϊm�Ļ���P���ɿ����ʵ㣩��B�����Ϸ�h=R�ߴ��ɾ�ֹ�ͷţ��������ٶ�Ϊg����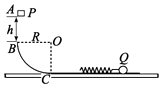
��1�����鵽��Բ�ι����͵�Cʱ���ٶȴ�С�ͶԹ����ѹ����
��2���ڻ���ѹ�����ɵĹ����У����ɾ��е���������ܣ�
��3���������B�Ϸ���H���ͷţ�ǡ��ʹ���龭���ɷ������ܹ��ص�B�㣬��߶�H�Ĵ�С��
���𰸡�
��1���⣺����P��A�˶���C���̣����ݻ�е���غ��
mg��h+R��= ![]()
��h=R�������� vC=2 ![]()
����͵�C�����Ի��飬����ţ�ٵڶ������У�FN��mg=m ![]()
��ù���Ի���P��֧���� FN=5mg
����ţ�ٵ�������֪����P�Թ����ѹ����СΪ5mg��������ֱ���£�
�𣺻��鵽��Բ�ι����͵�Cʱ���ٶȴ�С��2 ![]() ���Թ����ѹ����СΪ5mg��������ֱ���£�
���Թ����ѹ����СΪ5mg��������ֱ���£�
��2�����ɱ�ѹ�������У��������ٶ����ʱ�����ɾ�����������ܣ�����ϵͳ�����غ��У�mvC=��m+M��v
���ݻ�е���غ㶨���� ![]() =EPm+
=EPm+ ![]()
������� EPm= ![]() mgR
mgR
���ڻ���ѹ�����ɵĹ����У����ɾ��е������������ ![]() mgR��
mgR��
��3������P��B�Ϸ���h���ͷţ�����ˮƽ���ٶ�Ϊv0������
mg��H+R��= ![]() mv02��
mv02��
���ɱ�ѹ�����ٴλָ���ԭ��ʱ���軬��P��Q���ٶȴ�С�ֱ�Ϊv1��v2�����ݶ����غ��У�mv0=��mv1+Mv2
���ݻ�е���غ��� ![]() mv02=
mv02= ![]() mv12+
mv12+ ![]() Mv22
Mv22
Ҫʹ����P�����ɷ�����ǡ�ûص�B�㣬���� mgR= ![]() mv12
mv12
������� H=3R
�𣺸߶�H�Ĵ�С��3R��
����������1������P��A�˶���C�Ĺ��̣����ݻ�е���غ�����C��ʱ���ٶȣ�����͵�C����������Բ���˶�����������ṩ�������������Ի����֧���������ţ�ٵ���������⻬��Թ����ѹ����
��2�����ɱ�ѹ�������У���������������ģ�͵�����С�������Сʱ�������С���ٶ���ȣ����ɾ�����������ܣ�������Ϊ��������ϵͳ�����غ��ϻ�е���غ㶨����ʽ��⣻
��3������P��B�Ϸ���h���ͷţ����ݶ��ܶ����������ˮƽ����ٶȣ����ɱ�ѹ�����ٴλָ���ԭ���ù����У����ݶ����غ㶨���Լ���е���غ㶨����ʽ��P���ɷ�����ǡ�ûص�B��ù����У����ݶ��ܶ�����ʽ������������⣮

 �ŵ������ϵ�д�
�ŵ������ϵ�д�