题目内容
【题目】如图所示，斜面体固定不动，一轻质弹簧沿光滑斜面放置，下端固定在斜面底部挡板上．分两次将质量为m1、m2（m2＞m1）的两物块从斜面上不同位置静止释放，两次运动中弹簧的最大压缩量相同（弹簧始终在弹性限度范围内）．物块从开始释放到速度第一次减为零的过程，则（ ）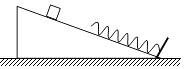
A.m1开始释放的高度高
B.m1的重力势能变化量大
C.m2的最大速度小
D.m2的最大加速度小
【答案】A,D
【解析】解：A、对任一物体，设物体的质量为m，物体从开始释放到速度第一次减为零下降的高度为h．取最低点所在水平面为参考平面．根据物体与弹簧组成的系统机械能守恒得：mgh=Ep，
据题，两次弹簧的最大弹性势能Ep相同，m2＞m1，则有h1＞h2．即m1开始释放的高度高，A符合题意．
B、物体从开始释放到速度第一次减为零的过程，物体的重力势能全部转化为弹簧的弹性势能，则两个物体重力势能变化量相等，B不符合题意．
C、物块的速度最大时，合力为零，则有 kx=mgsinα，因为m2＞m1，所以x2＞x1．
设弹簧的最大压缩量为xm．物块刚下滑时离弹簧的距离为L．从开始到最低点的过程，根据能量守恒定律得：
Ep=mgsinα（xm+L），由题知，xm、Ep相等，m2＞m1，则 L2＜L1．
从开始到速度最大的过程，由能量守恒得：mgsinα（L+x）= 
+ 
kx2，又 x= 
，解得：vm= 
，由于m2＞m1，L2＜L1，可知不能判断最大速度的大小．C不符合题意．
D、两次运动中弹簧的最大压缩量相同，弹簧的最大弹力相同，设为F，由牛顿第二定律得 F﹣mgsinα=ma，得最大加速度为 a= 
﹣gsinα，由于m2＞m1，所以m2的最大加速度小于m1的最大加速度，D符合题意．
故答案为：AD
首先，明确两次变化过程中，弹簧最大弹性势能相同。根据机械能守恒定律，列式求解。
