Question

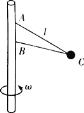
【题目】如图所示，两绳系一个质量为m的小球。两绳的另两端分别固定于竖直轴上的A、B两处，绳AC长为L。两绳都拉直时，AC与轴夹角为α，BC与轴夹角为β，已知重力加速度大小为g。问：

(1)小球绕轴做圆周运动的角速度在什么范围内，两绳都能拉直？

(2)当两绳都受到拉力，且角速度为ω0时，上、下两绳对小球的拉力分别为多大？

Answer 1

【答案】(1)；(2)，

【解析】

(1)当AC绳拉直但没有力时，即FT1=0时，由重力和绳BC的拉力FT2的合力提供向心力，根据牛顿第二定律，有

其中

联立解得

当FT2恰为零时，根据牛顿第二定律，有

其中

联立解得

则两绳均张紧时角速度范围为

(2)两绳均处于张紧状态，此时小球受FT1、FT2、mg三力作用，正交分解后可得，水平方向

竖直方向

联立解得