题目内容
有三颗质量相同的人造地球卫星1、2、3，其中1是放置在赤道附近还未发射的卫星，2是靠近地球表面做圆周运动的卫星，3是在高空的一颗地球同步卫星。比较这三颗人造卫星的角速度ω，下列判断正确的是
| A．ω1=ω2 | B．ω1<ω2 | C．ω1> ω3 | D．ω2< ω3 |
B
解析试题分析：由题意地球同步卫星3周期与地球自转周期相同，即与放在赤道的卫星1的周期相同，根据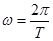
可知，地球同步卫星3和放在赤道的卫星1的角速度也是相等的，即
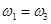，对表面卫星2与同步卫3，由
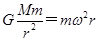，得
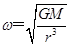可知，卫星3的角速度小于卫星2的角速度，即
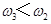，所以
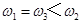，B正确．
考点：万有引力定律的应用
练习册系列答案
阅读快车系列答案
相关题目
一只小船在静水中的速度为3m／s，它要渡过一条宽为30m的河，河水流速为4m／s，则这只船：
| A．过河时间不可能小于10s |
| B．不能沿垂直于河岸方向过河 |
| C．可以渡过这条河，而且所需时间可以为6s |
| D．不可能渡过这条河 |
关于地球同步卫星，以下说法：①和地球公转具有相同的周期；②只能在赤道的正上方；③做匀速圆周运动，合外力为零；④离地心的距离是一定值。以上说法中正确的有：
| A．①③ | B．①④ | C．②③ | D．②④ |
如图所示，a，b两颗质量相同的人造地球卫星分别在半径不同的轨道上绕地球作匀速圆周运动，则
| A．卫星a的周期大于卫星b的周期 |
| B．卫星a的动能大于卫星b的动能 |
| C．卫星a的势能大于卫星b的势能 |
| D．卫星a的加速度大于卫星b的加速度 |
两质量之比为
的卫星绕地球做匀速圆周运动，运动的轨道半径之比
，则下列关于两颗卫星的说法中正确的是
A．线速度大小之比为 |
B．向心加速度大小之比为 |
C．运动的周期之比为 |
D．动能之比为 |
太阳质量为M，地球质量为m，地球绕太阳公转的周期为T，万有引力恒量值为G，地球公转半径为R，地球表面重力加速度为g．则以下计算式中正确的是
| A．地球公转所需的向心力为F向＝mg | B．地球公转半径 |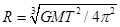
C．地球公转的角速度 | D．地球公转的向心加速度  |
关于环绕地球运行的卫星，下列说法正确的是( )
| A．分别沿圆轨道和椭圆轨道运行的两颗卫星，不可能具有相同的周期 |
| B．在赤道上空运行的两颗地球同步卫星，它们的轨道半径有可能不同 |
| C．沿椭圆轨道运行的一颗卫星，在轨道不同位置可能具有相同的速率 |
| D．沿不同轨道经过北京上空的两颗卫星，它们的轨道平面一定会重合 |
据美国媒体报道，美国和俄罗斯的两颗卫星在西伯利亚上空相撞．这是人类有史以来的首次卫星碰撞事件．碰撞发生的地点位于西伯利亚上空490英里(约790公里)，恰好比国际空间站的轨道高270英里（434公里）．若卫星和空间站轨道均可视为圆轨道，则以下相关说法中不正确的是（ ）
| A．碰撞后的碎片若受到稀薄大气的阻力作用，轨道半径将变小，则有可能与国际空间站相碰撞 |
| B．在碰撞轨道上运行的卫星的周期比国际空间站的周期小 |
| C．发射一颗到碰撞轨道运行的卫星，则发射速度要大于第一宇宙速度7.9 km/s |
| D．同一个圆轨道上，若后面的卫星一旦加速，将有可能与前面的卫星相碰撞 |