题目内容
20.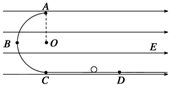 如图所示,ABCD为竖直放在场强为E=104 N/C的水平匀强电场中的绝缘光滑轨道,其中轨道的ABC部分是半径为R=0.5m的半圆环(B为半圆弧的中点),轨道的水平部分与半圆环相切于C点,D为水平轨道的一点,而且CD=2R,把一质量m=100g、带电荷量q=10-4 C的负电小球,放在水平轨道的D点,由静止释放后,
如图所示,ABCD为竖直放在场强为E=104 N/C的水平匀强电场中的绝缘光滑轨道,其中轨道的ABC部分是半径为R=0.5m的半圆环(B为半圆弧的中点),轨道的水平部分与半圆环相切于C点,D为水平轨道的一点,而且CD=2R,把一质量m=100g、带电荷量q=10-4 C的负电小球,放在水平轨道的D点,由静止释放后,小球在轨道的内侧运动.g=10m/s2,求:
(1)它到达B点时的速度是多大?
(2)它到达B点时对轨道的压力是多大?
分析 (1)应用动能定理研究小球由,D→B的过程,求出小球在B点的速度大小,
(2)对小球在B点进行受力分析,找出径向提供向心力的外力,应用牛顿第二定律求解球受到的支持力,再由牛顿第三定律求解压力.
解答 解:(1)设:小球在B点的速度大小是VB,则对于小球由D→B的过程中,应用动能定理列出:
qE×3R-mgR=$\frac{1}{2}$mvB2
解得:vB=2$\sqrt{5}$m/s
(2)则球受到轨道的压力大小为NB,在B点的圆轨道径向方向上,小球受到轨道对它的弹力和电场力,应用牛顿第二定律,有:
NB-qE=m$\frac{{v}_{B}^{2}}{R}$
解得:NB=5×104×10-4+0.1×$\frac{(2\sqrt{5})^{2}}{0.5}$=5N
由牛顿第三定律可知,它对轨道的压力为5N.
答:(1)它到达B点时的速度是2$\sqrt{5}$m/s
(2)它到达B点时对轨道压力是5N
点评 在本题中物体不仅受重力的作用,还有电场力,在解题的过程中,一定要分析清楚物体的受力和运动过程,根据动能定理和牛顿第二定律灵活列式求解.

练习册系列答案
相关题目
10. 如图所示,理想变压器原、副线圈的匝数比为20:1,b接原线圈的中心抽头,电压表和电流表均为理想电表.从某时刻开始在原线圈c、d两端加上交变电压,其瞬时值表达式为u=220×2${\;}^{\frac{1}{2}}$sin100πt(V),则( )
如图所示,理想变压器原、副线圈的匝数比为20:1,b接原线圈的中心抽头,电压表和电流表均为理想电表.从某时刻开始在原线圈c、d两端加上交变电压,其瞬时值表达式为u=220×2${\;}^{\frac{1}{2}}$sin100πt(V),则( )
 如图所示,理想变压器原、副线圈的匝数比为20:1,b接原线圈的中心抽头,电压表和电流表均为理想电表.从某时刻开始在原线圈c、d两端加上交变电压,其瞬时值表达式为u=220×2${\;}^{\frac{1}{2}}$sin100πt(V),则( )
如图所示,理想变压器原、副线圈的匝数比为20:1,b接原线圈的中心抽头,电压表和电流表均为理想电表.从某时刻开始在原线圈c、d两端加上交变电压,其瞬时值表达式为u=220×2${\;}^{\frac{1}{2}}$sin100πt(V),则( )| A. | 单刀双掷开关与a连接,在滑动变阻器触头P向上移动的过程中,电压表和电流表的示数均变小 | |
| B. | 原线圈和副线圈中交变电流的频率之比为20:l | |
| C. | 当单刀双掷开关与b连接时,电压表的示数为22V | |
| D. | 当单刀双掷开关由a扳向b后,电压表和电流表的示数均变小 |
8.关于打点计时器,回答下列问题
(1)电磁打点计时器使用的是A电源
(2)某同学利用电火花打点计时器测定小车作匀变速运动的加速度,实验中不需要的器材是③⑦(用代号表示)
①电火花打点计时器②刻度尺③秒表④带滑轮长木板⑤小车⑥纸带⑦天平
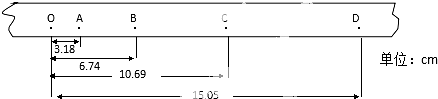
(3)某同学利用打点计时器所记录的纸带来研究做匀变速直线运动小车的运动情况.实验中获得一条纸带如图所示.其中两相邻的计数点间有四个点未画出.已知所用电源的频率为50Hz,则相邻两个计数点间的时间为0.1s,打A点时小车运动的速度VA=0.337m/s;小车运动的加速度a=0.393m/s2.(后两空保留三位有效数字)
(1)电磁打点计时器使用的是A电源
| A、低压交流 | B、低压直流 | C、220V交流电源 |
①电火花打点计时器②刻度尺③秒表④带滑轮长木板⑤小车⑥纸带⑦天平
(3)某同学利用打点计时器所记录的纸带来研究做匀变速直线运动小车的运动情况.实验中获得一条纸带如图所示.其中两相邻的计数点间有四个点未画出.已知所用电源的频率为50Hz,则相邻两个计数点间的时间为0.1s,打A点时小车运动的速度VA=0.337m/s;小车运动的加速度a=0.393m/s2.(后两空保留三位有效数字)

12.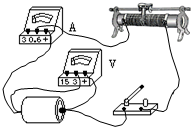 某同学用电流表和电压表测一节干电池的电动势和内电阻,所用滑动变阻器的阻值范围为0-20Ω,电路的实物图如图所示.该同学接线中错误和不规范的做法是( )
某同学用电流表和电压表测一节干电池的电动势和内电阻,所用滑动变阻器的阻值范围为0-20Ω,电路的实物图如图所示.该同学接线中错误和不规范的做法是( )
 某同学用电流表和电压表测一节干电池的电动势和内电阻,所用滑动变阻器的阻值范围为0-20Ω,电路的实物图如图所示.该同学接线中错误和不规范的做法是( )
某同学用电流表和电压表测一节干电池的电动势和内电阻,所用滑动变阻器的阻值范围为0-20Ω,电路的实物图如图所示.该同学接线中错误和不规范的做法是( )| A. | 滑动变阻器不起变阻作用 | B. | 电流表接线错误 | ||
| C. | 电压表量程选用不当 | D. | 电压表接线有错 |
9.如图甲所示是一种速度传感器的工作原理图,在这个系统中B为一个能发射超声波的固定小盒子,工作时小盒子B向被测物体发出短暂的超声波脉冲,脉冲被运动的物体反射后又被B盒接收,从B盒发射超声波开始计时,经时间△t0再次发射超声波脉冲,图乙是连续两次发射的超声波的位移-时间图象,则下列说法正确的是( )
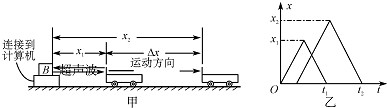

| A. | 超声波的速度为$\frac{2{x}_{1}}{{t}_{1}}$ | |
| B. | 物体的平均速度为$\frac{2({x}_{2}-{x}_{1})}{({t}_{2}-{t}_{1}+2△{t}_{0})}$ | |
| C. | 超声波的速度为$\frac{2{x}_{2}}{{t}_{2}}$ | |
| D. | 物体的平均速度为$\frac{2({x}_{2}-{x}_{1})}{({t}_{2}-{t}_{1}+△{t}_{0})}$ |
10.在静电场中,下列有关电势能、电势判断错误的是( )
| A. | 电势能、电势都是仅有电场本身因素决定,与处于电场中的电荷无关 | |
| B. | 电势高的地方,电荷的电势能一定大 | |
| C. | 顺着电场线运动,电荷的电势能一定减少 | |
| D. | 某点电势的大小等于单位电荷在该点与在参考点的电势能差的大小 |