题目内容
9.两个星球半径之比2:3,表面重力加速度之比1:2,求:(1)两个星球质量之比;
(2)两个星球上第一宇宙速度之比.
分析 根据星球表面重力等于万有引力求星球质量之比;
根据万有引力提供近地轨道卫星的向心力求第一宇宙速度之比;
解答 解:(1)根据星球表面重力等于万有引力有:
mg=G$\frac{mM}{{R}^{2}}$
解得:M=$\frac{{gR}^{2}}{G}$
两个星球半径之比2:3,表面重力加速度之比1:2,
所以两个星球质量之比是2:9,
(2)行星表面的环绕速度即为第一宇宙速度,做匀速圆周运动的向心力是万有引力提供的,则有:
G$\frac{mM}{{R}^{2}}$=m$\frac{{v}^{2}}{R}$
解得:v=$\sqrt{\frac{GM}{R}}$=$\sqrt{gR}$,
两个星球半径之比2:3,表面重力加速度之比1:2,
所以两个星球上第一宇宙速度之比是1:$\sqrt{3}$,
答:(1)两个星球质量之比是2:9;
(2)两个星球上第一宇宙速度之比是1:$\sqrt{3}$.
点评 对于卫星问题,常常根据万有引力等于重力求星球表面的重力加速度,由万有引力等于向心力求其速度.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
14.光滑的水平面上固定一光滑的柱子,一根细线的一端固定在柱子上,另一端系着一光滑的小球,细线处于伸直状态.现给小球一垂直于细线的速度,使小球绕柱子转动,在整个过程中,细线始终垂直于小球的速度,最终细线完全绕在柱子上.在该过程中,下列说法正确的是( )
| A. | 小球运动的线速度越来越大 | B. | 小球运动的加速度越来越大 | ||
| C. | 小球运动的角速度越来越大 | D. | 细线的拉力越来越大 |
13.“神州八号”与“天宫一号”对接前各自绕地球运动,设“天宫一号”在半径为r1的圆轨道上运动,周期为T1,“神州八号”在半径为r2的圆轨道上运动,r1>r2,则( )
| A. | “天宫一号”的运行速度大于7.9km/s | |
| B. | “神州八号”的周期为T2=T1$\sqrt{\frac{{{r}_{2}}^{3}}{{{r}_{1}}^{3}}}$ | |
| C. | 地球的质量为$M=\frac{{4{π^2}r_1^3}}{GT_1^2}$ | |
| D. | 地球表面的重力加速度为$g=\frac{{4{π^2}{r_1}}}{T_1^2}$ |
 质量M=2kg的小平板车静止在光滑水平面上,车的一端静止着质量为mA=2kg的物体A(可视为质点),如图所示.一颗质量为mB=20g的子弹以600m/s的水平速度迅速射穿A后,速度变为100m/s最后物体A仍静止在车上.若物体A与小车间的滑动摩擦系数μ=0.5,取g=10m/s2,求:
质量M=2kg的小平板车静止在光滑水平面上,车的一端静止着质量为mA=2kg的物体A(可视为质点),如图所示.一颗质量为mB=20g的子弹以600m/s的水平速度迅速射穿A后,速度变为100m/s最后物体A仍静止在车上.若物体A与小车间的滑动摩擦系数μ=0.5,取g=10m/s2,求: “心”形导线框固定在匀强磁场中,磁感线的方向与导线框所在平面垂直,规定磁场的正方向垂直纸面向里,磁感应强度B随时间变化的规律如图所示.若规定顺时针方向为感应电流I的正方向,下列各图中正确的是( )
“心”形导线框固定在匀强磁场中,磁感线的方向与导线框所在平面垂直,规定磁场的正方向垂直纸面向里,磁感应强度B随时间变化的规律如图所示.若规定顺时针方向为感应电流I的正方向,下列各图中正确的是( )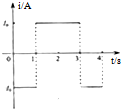



 如图所示,物体由斜面上高为h的A位置滑下来,滑到平面上的另一点C停下来,若斜面与水平面的材料相同,且斜面与水平面在B处平滑连接,s是释放点到停止点的水平总距离,试证明:物体与滑动面之间 动摩擦因数μ与s,h之间存在关系μ=$\frac{h}{s}$.
如图所示,物体由斜面上高为h的A位置滑下来,滑到平面上的另一点C停下来,若斜面与水平面的材料相同,且斜面与水平面在B处平滑连接,s是释放点到停止点的水平总距离,试证明:物体与滑动面之间 动摩擦因数μ与s,h之间存在关系μ=$\frac{h}{s}$. ):绕制螺线管金属丝的电阻率ρ=5.0×10-7Ω•m,电阻RL约为100Ω
):绕制螺线管金属丝的电阻率ρ=5.0×10-7Ω•m,电阻RL约为100Ω