ĢāÄæÄŚČŻ
”¾ĢāÄæ”æijæÕ¼äÕ¾ŌŚ°ė¾¶ĪŖRµÄŌ²ŠĪ¹ģµĄÉĻŌĖŠŠ£¬ÖÜĘŚĪŖT”£ĮķÓŠŅ»·É“¬ŌŚ°ė¾¶ĪŖrµÄŌ²ŠĪ¹ģµĄÉĻŌĖŠŠ£¬·É“¬ÓėæÕ¼äÕ¾µÄČĘŠŠ·½ĻņĻąĶ¬”£µ±æÕ¼äÕ¾ŌĖŠŠµ½AµćŹ±£¬·É“¬Ē”ŗĆŌĖŠŠµ½Bµć£¬A”¢BÓėµŲŠÄĮ¬ĻßĻą»„“¹Ö±£¬“ĖŹ±·É“¬¾¼«¶ĢŹ±¼äµÄµć»š¼ÓĖŁ£¬±ä»ÆŗóµÄĶÖŌ²¹ģµĄ½üµŲµćĪŖB£¬Ō¶µŲµćÓėæÕ¼äÕ¾µÄ¹ģµĄĻąĒŠÓŚCµć£¬ČēĶ¼ĖłŹ¾”£µ±·É“¬µŚŅ»“Īµ½“ļCµćŹ±£¬Ē”ŗĆÓėæÕ¼äÕ¾ĻąÓö”£ÓÉŅŌÉĻŠÅĻ¢æÉÅŠ¶Ø
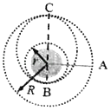
A. æÕ¼äÕ¾µÄ¶ÆÄÜŠ”ÓŚ·É“¬ŌŚ°ė¾¶ĪŖrµÄŌ²ŠĪ¹ģµĄÉĻŌĖŠŠŹ±µÄ¶ÆÄÜ
B. µ±·É“¬ÓėæÕ¼äÕ¾ĻąÓöŹ±£¬æÕ¼äÕ¾µÄ¼ÓĖŁ¶Č“óÓŚ·É“¬µÄ¼ÓĖŁ¶Č
C. ·É“¬ŌŚ“ÓBµćŌĖ¶Æµ½CµćµÄ¹ż³ĢÖŠ£¬ĖŁ¶Č±ä“ó
D. æÕ¼äÕ¾µÄŌ²ŠĪ¹ģµĄ°ė¾¶RÓė·É“¬µÄŌ²ŠĪ¹ģµĄ°ė¾¶rµÄ¹ŲĻµĀś×ć![]()
”¾“š°ø”æD
”¾½āĪö”æ
A”¢µ±æÕ¼äÕ¾ŗĶ·É“¬¾ł×öŌ²ÖÜŌĖ¶ÆŹ±£¬ĘäĶņÓŠŅżĮ¦Ģį¹©ĻņŠÄĮ¦£¬¼“![]() £¬ŌņĻßĖŁ¶Č“óŠ”ĪŖ£ŗ
£¬ŌņĻßĖŁ¶Č“óŠ”ĪŖ£ŗ![]() £¬ÓÉÓŚæÕ¼äÕ¾µÄ°ė¾¶“óÓŚ·É“¬µÄ°ė¾¶£¬¹ŹæÕ¼äÕ¾µÄĖŁ¶ČµÄ“󊔊”ÓŚ·É“¬µÄĖŁ¶Č“󊔣¬ÓÉÓŚ¶žÕßµÄÖŹĮæ¹ŲĻµĪ“ÖŖ£¬¹Źøł¾Ż¶ÆÄܵĹ«Ź½
£¬ÓÉÓŚæÕ¼äÕ¾µÄ°ė¾¶“óÓŚ·É“¬µÄ°ė¾¶£¬¹ŹæÕ¼äÕ¾µÄĖŁ¶ČµÄ“󊔊”ÓŚ·É“¬µÄĖŁ¶Č“󊔣¬ÓÉÓŚ¶žÕßµÄÖŹĮæ¹ŲĻµĪ“ÖŖ£¬¹Źøł¾Ż¶ÆÄܵĹ«Ź½![]() ĪŽ·ØÅŠ¶Ļ¶žÕߵĶÆÄܓ󊔹ŲĻµ£¬¹ŹA“ķĪó£»
ĪŽ·ØÅŠ¶Ļ¶žÕߵĶÆÄܓ󊔹ŲĻµ£¬¹ŹA“ķĪó£»
B”¢µ±·É“¬ÓėæÕ¼äÕ¾ĻąÓöŹ±£¬øł¾ŻÅ£¶ŁµŚ¶ž¶ØĀÉÓŠ£ŗ![]() £¬¼“
£¬¼“![]() £¬æÉÖŖ¶žÕßĻąÓöŹ±Ęä¼ÓĖŁ¶ČµÄ“óŠ”ĻąµČ£¬¹ŹB“ķĪó£»
£¬æÉÖŖ¶žÕßĻąÓöŹ±Ęä¼ÓĖŁ¶ČµÄ“óŠ”ĻąµČ£¬¹ŹB“ķĪó£»
C”¢øł¾ŻæŖĘÕĄÕµŚ¶ž¶ØĀÉæÉÖŖ£¬·É“¬ŌŚ“ÓBµćŌĖ¶Æµ½CµćµÄ¹ż³ĢÖŠ£¬ĖŁĀŹŌ½Ą“Ō½Š”£¬¹ŹC“ķĪó£»
D”¢Éč·É“¬ĶÖŌ²¹ģµĄµÄÖÜĘŚĪŖT”䣬Ōņøł¾ŻæŖĘÕĄÕµŚČż¶ØĀÉæÉÖŖ£ŗ![]() ÓÉĢāæÉÖŖ£ŗ
ÓÉĢāæÉÖŖ£ŗ![]() £¬ĮŖĮ¢æÉŅŌµĆµ½£ŗ
£¬ĮŖĮ¢æÉŅŌµĆµ½£ŗ![]() £¬¹ŹDÕżČ·”£
£¬¹ŹDÕżČ·”£

 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø