题目内容
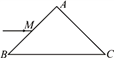
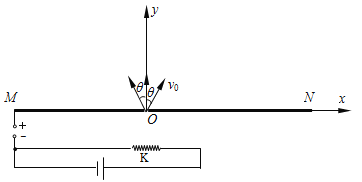
【题目】如图所示,一个半径为r、粗细均匀、阻值为R的圆形导线框,竖直放置在磁感应强度为B的水平匀强磁场中,线框平面与磁场方向垂直。现有一根质量为m、电阻不计的导体棒,自圆形线框最高点由静止释放,棒在下落过程中始终与线框保持良好接触。已知下落距离为![]() 时棒的速度大小为v1,下落到圆心O时棒的速度大小为v2,忽略摩擦及空气阻力,下列说法正确的是
时棒的速度大小为v1,下落到圆心O时棒的速度大小为v2,忽略摩擦及空气阻力,下列说法正确的是

A. 导体棒下落距离为![]() 时,棒中感应电流的方向向右
时,棒中感应电流的方向向右
B. 导体棒下落距离为![]() 时,棒的加速度的大小为
时,棒的加速度的大小为![]()
C. 导体棒下落到圆心时,圆形导线框的发热功率为![]()
D. 导体棒从开始下落到经过圆心的过程中,圆形导线框产生的热量为![]()
【答案】BD
【解析】A项:导体棒下落过程中切割磁感线,根据右手定则可知,棒中感应电流的方向向左,故A错误;
B项:棒下落距离为![]() ,时,棒有效的切割长度为L=2rcos30°=
,时,棒有效的切割长度为L=2rcos30°= ![]() ,弦所对的圆心角为120°,则圆环上半部分的电阻为
,弦所对的圆心角为120°,则圆环上半部分的电阻为![]() ,圆环下半部分的电阻为
,圆环下半部分的电阻为![]()
由外电路并联电阻为: 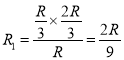
此时,回路中感应电动势为 E=BLv, ![]() ,安培力F=BIL,
,安培力F=BIL,
联立得: 
由牛顿第二定律得:mg-F=ma
得: ![]() ,故B正确;
,故B正确;
C项:导体棒下落到圆心时,棒有效的切割长度为2r,回路中的总电阻为![]() ,电动势为
,电动势为![]() ,根据公式
,根据公式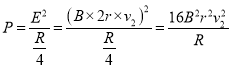 ,故C错误;
,故C错误;
D项:从开始下落到经过圆心的过程中,棒的重力势能减小转化为棒的动能和内能,根据能量守恒定律得:
![]() ,解得
,解得![]() ,故D正确。
,故D正确。
点晴:对于电磁感应问题,常常从两个角度研究:一是力的角度,关键是安培力的分析和计算;二是能量的角度,根据能量守恒定律研究。

练习册系列答案
相关题目