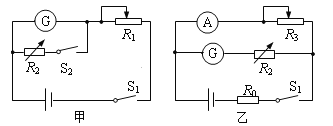
题目内容
【题目】如图所示,金属平板MN垂直于纸面放置,MN板中央有小孔O,以O为原点在纸面内建立xOy坐标系,x轴与MN板重合。O点下方的热阴极K通电后能持续放出初速度近似为零的电子,在K与MN板间加一电压,从O点射出的电子速度大小都是v0,方向在纸面内,且关于y轴对称,发散角为2θ弧度。已知电子电荷量为e,质量为m,不计电子间相互作用及重力的影响。
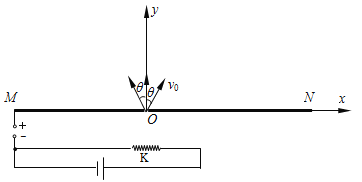
(1)求K与MN间的电压的大小U0。
(2)若x轴上方存在范围足够大的垂直纸面向里的匀强磁场,电子打到x轴上落点范围长度为△x,求该磁场的磁感强度B1和电子从O点到达x轴最短时间t。
(3)若x轴上方存在一个垂直纸面向里的圆形匀强磁场区,电子从O点进入磁场区偏转后成为一宽度为△y、平行于x轴的电子束,求该圆形区域的半径R及磁场的磁感强度B2。
【答案】(1) ![]() (2)
(2) ![]() ,
, ![]() (3)
(3) ![]() ,
,![]()
【解析】试题分析:在电场中根据动能定理即可求出K与MN板间的电压U0;画出粒子运动轨迹,根据洛伦兹力提供向心力和几何关系即可求出磁场感应强度B1和电子从O点到达x轴最短时间;若x轴上方存在一个垂直纸面向里的圆形匀强磁场区,电子从O点进入磁场,画出粒子运动轨迹,根据洛伦兹力提供向心力和几何关系即可求出磁场感应强度和半径。
(1) 由动能定理有: ![]()
解得: ![]()
(2) 粒子运动轨迹如图所示:
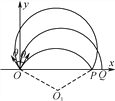
从O点射出的电子落在x轴PQ间,设电子做圆周运动半径为r,由几何关系有
Δx=2r-2rcos θ
由向心力公式有: ![]()
解得: ![]()
最短路程为: ![]()
则有: ![]()
(3) 电子运动轨迹如图所示:
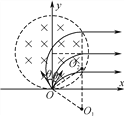
由几何关系可知r=R
且有Δy=(r+rsin θ)-(r-rsin θ)=2rsin θ
解得: ![]()
由向心力公式有: ![]()
解得: ![]()

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目