题目内容
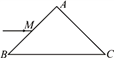
【题目】如图所示，一个三棱镜的截面为等腰直角△ABC，腰长为a，∠A＝90°。一束细光线沿此截面所在平面且平行于BC边的方向射到AB边上的中点，光进入棱镜后直接射到AC边上，并刚好能发生全反射。已知真空中的光速为c，试求：
(i)该棱镜材料的折射率n；
(ii)光从AB边到AC边的传播时间t。
【答案】(1) 
（2）
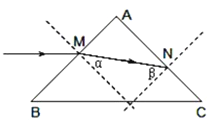
【解析】【试题分析】作出在AC面恰好发生全反射时的光路图，结合折射定律并抓住AB面的折射角与AC面入射角之和为90°求解该棱镜材料的折射率；由几何关系求出光子AB与AC之间传播的距离，然后结合
求出光在介质中的速度，最后由x=vt即可求出时间．
(1)设光从AB边射入时折射角为α，射到AC面上N点时入射角为
，光路如图：
根据折射定律： 
得： 
①
光在AC边上恰好发生全反射： 
②
又由几何关系：α+β=90°
则sin2α+sin2β=1 ③
将①②代入③解得： 
(2)由图中几何关系可得M、N间距： 
由①可得： 
用v表示光在棱镜内传播的速度： 
光从AB边到AC边的传播时间： 
练习册系列答案
阶梯计算系列答案
相关题目
