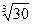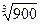题目内容
已知某星球的半径为R,有一距星球表面高度h=R处的卫星,绕该星球做匀速圆周运动,测得其周期T=2π
.求:
(1)该星球表面的重力加速度g
(2)若在该星球表面有一如图所示的装置,其中AB部分为一长为12.8m并以5m/s速度顺时针匀速转动的传送带,BCD部分为一半径为1.6m竖直放置的光滑半圆形轨道,直径BD恰好竖直,并与传送带相切于B点.现将一质量为0.1kg的可视为质点的小滑块无初速地放在传送带的左端A点上,已知滑块与传送带间的动摩擦因数为0.5.
试求出到达D点时对轨道的压力大小;(提示:
=3.2)

| 5R |
(1)该星球表面的重力加速度g
(2)若在该星球表面有一如图所示的装置,其中AB部分为一长为12.8m并以5m/s速度顺时针匀速转动的传送带,BCD部分为一半径为1.6m竖直放置的光滑半圆形轨道,直径BD恰好竖直,并与传送带相切于B点.现将一质量为0.1kg的可视为质点的小滑块无初速地放在传送带的左端A点上,已知滑块与传送带间的动摩擦因数为0.5.
试求出到达D点时对轨道的压力大小;(提示:
| 10.24 |

(1)对距星球表面h=R处的卫星(设其质量为m),
有:G
| Mm |
| (R+h)2 |
| 2π |
| T |
对在星球表面的物体m′,有:G
| Mm′ |
| R2 |
解得:g=1.6m/s2
(2)设滑块从A到B一直被加速,且设到达B点时的速度为VB
则:VB=
| 2ax |
| 2μgx |
| 2×0.5×1.6×12.8 |
| 16 |
| 5 |
| 2 |
| 2 |
因VB<5m/s,故滑块一直被加速
设滑块能到达D点,且设到达D点时的速度为VD
则在B到D的过程中,由动能定理:-mg?2R=
| 1 |
| 2 |
| 1 |
| 2 |
解得:VD=
|
| 3.22×2-4×1.6×1.6 |
而滑块能到达D点的临界速度:V0=
| gR |
即滑块能到达D点
在D点时由重力和轨道的压力共同提供向心力:
N+mg=m
| vD2 |
| R |
解得:
N=0.48N
由牛顿第三定律知,物体对轨道的压力为0.48N
答:
(1)星球表面的重力加速度为1.6m/s2
(2)在D点对轨道的压力为0.48N

练习册系列答案
相关题目
 ,靠近行星表面的卫星,其运行周期为T,试证明
,靠近行星表面的卫星,其运行周期为T,试证明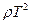 为一常数。
为一常数。