题目内容
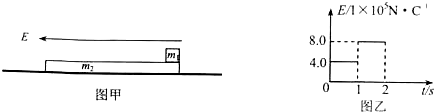
如图1所示,平行板电容器带电量为Q,固定在绝缘底座上,两极板竖直放置,整个装置静止在光滑的水平面上,板间距离为d,一个质量为m,带电量为+q的弹丸以一定的初速度从一极板间中点的小孔射入电容器中(弹丸的重力不计,电容器外面周围的电场强度为零),设弹丸在电容器中最远运动到P点,弹丸在整个运动过程中的v-t图象如图2所示,根据力学规律和题中所提供的信息,你能求得哪些定量的结果?请写出其中四个物理量的求解过程.提示:例如反映电容器的有关物理量、电容器及底座的总质量及系统在运动过程中的守恒量等.


答案有多种
(1)从题中v-t图象提供信息可知,弹丸在电容器内两平行板间电场力作用下先做匀减速直线运动,速度减为零后,再向右做匀加速直线运动,在t1时刻刚好离开电容器,做匀速运动,速度为v1.
从图象可得弹丸的加速度大小为:a=
(2)设电场强度为E,由牛顿定律得qE=ma
解得:E=
(3)电容器电压U=Ed=
d
(4)电容器的电容C=
=
(5)设电容器最后速度为v,电容器及底座总质量为M,
由动量定恒:mv0=Mv-mv1
能量守恒:
m
=
MV2+
m
解得:电容器及底座总质量为M=
(6)弹丸及电容器组成的系统在整个运动过程中,能量守恒:
弹丸及电容器的总能量E0=
m
(1)从题中v-t图象提供信息可知,弹丸在电容器内两平行板间电场力作用下先做匀减速直线运动,速度减为零后,再向右做匀加速直线运动,在t1时刻刚好离开电容器,做匀速运动,速度为v1.
从图象可得弹丸的加速度大小为:a=
| v0+v1 |
| t1 |
(2)设电场强度为E,由牛顿定律得qE=ma
解得:E=
| m(v0+v1) |
| qt1 |
(3)电容器电压U=Ed=
| m(v0+v1) |
| qt1 |
(4)电容器的电容C=
| Q |
| U |
| qQt1 |
| m(v0+v1)d |
(5)设电容器最后速度为v,电容器及底座总质量为M,
由动量定恒:mv0=Mv-mv1
能量守恒:
| 1 |
| 2 |
| v | 20 |
| 1 |
| 2 |
| 1 |
| 2 |
| v | 21 |
解得:电容器及底座总质量为M=
| m(v0+v1) |
| v0-v1 |
(6)弹丸及电容器组成的系统在整个运动过程中,能量守恒:
弹丸及电容器的总能量E0=
| 1 |
| 2 |
| v | 20 |

练习册系列答案
相关题目