Question

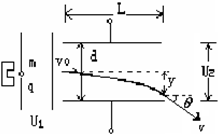
如图所示，有一质子（质量为m，电荷量为e）由静止开始经电压为U₁的电场的加速后，进入两块板间距离为d、板间电压为U₂的平行金属板间，若质子恰好从两板正中间垂直电场方向射入偏转电场，求：（不计质子的重力）
（1）质子进入偏转电场时的速度；
（2）为保证质子能从下极板正中央的小孔射出，则极板的长度应为多少？

Answer 1

（1）根据动能定理得：eU1=

1

2

mv2
解得：v=

2eU1 m

（2）水平方向有：x=

L

2

=vt
竖直方向有：y=

d

2

=

1

2

at2
根据匀强电场的场强公式有：E=

U2

d

根据牛顿第二定律得：a=

eE

m

联立解得：L=2d

2U1 U2

．
答：（1）质子进入偏转电场时的速度为v=

2eU1 m

（2）极板的长度应为L=2d

2U1 U2

．