Question

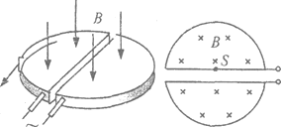
【题目】如图所示，在一个圆形区域内，两个方向相反且都垂直于纸面的匀强磁场分布在以直径为边界的两个半圆形区域Ⅰ、Ⅱ中，已知与的夹角为一质量为m、带电量为的粒子以某一速度从Ⅰ区的边缘点处沿与成角的方向射入磁场，随后该粒子以垂直于的方向经过圆心O进入Ⅱ区，最后再从处射出磁场若忽略该粒子重力，则下列说法正确的是　　

A. 粒子在磁场区域Ⅰ、Ⅱ中的半径和之比为2：1

B. 粒子在磁场区域Ⅰ、Ⅱ中圆周运动的周期和之比为1：2

C. 粒子在磁场区域Ⅰ、Ⅱ中所用的时间和之比为2：1

D. 粒子在磁场区域Ⅰ、Ⅱ中的磁感应强度大小和之比为1：2

Answer 1

【答案】AD

【解析】

带电粒子才Ⅰ区以垂直于的方向经过圆心O进入Ⅱ区，最后再从处射出磁场，由此画出粒子运动的轨迹，找出圆心，确定半径和偏转角，最后根据洛伦兹力提供向心力得到半径公式，周期公式以及所转过的圆心角逐项分析即可．

设圆形区域的半径为R，画出粒子运动轨迹的示意图，分析可知Ⅰ、Ⅱ中的半径，，故：：1，故A正确；根据周期公式可得：，，又因：：：1，所以：：1，故B错误；粒子在磁场区域Ⅰ、Ⅱ中所用的时间：，，又因：：1，所以：：3，故C错误；根据周期公式：，，可知：：2，故D正确。故选AD。