题目内容
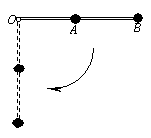
如图所示,一根轻杆长为2 l, 它的左端O点为固定转动轴, 轻杆可以绕 O轴在竖直平面内无摩擦转动, 它的中点及右端各固定一个小球A和B, 两球的质量分别是m和 2 m , 重力加速度为g。现用外力使杆处于水平位置, 从静止释放。求从开始运动到达杆处于竖直位置的过程中, 杆的作用力对B球所做的功。

首先我们分析在这个过程中,杆的弹力为什么对B球做功。设想如果A.B两球是分别固定在两个杆上的,同时释放,一定是A球先到达最低位置,现在两球在同一杆上,要同时到达最低点,必然是A球受杆的影响而变慢,B球受杆的影响而变快。也就是说在这过程中杆要发生弯曲形变,从而分别对两球做功,对A球做的是负功,对B球做的是正功。具体求解过程如下:
设没有A球,B球下落至最低点时速度大小为v1, 有A球后,B球下落至最低点时速度大小为v2。根据机械能守恒定律,可得
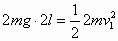 ,
, 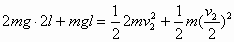 ,
,则杆对B球做的功等于B球在这两种情况下的动能之差,即
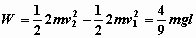 。
。
练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
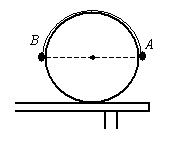
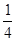 圆弧形轨道,圆弧半径为R,O为圆心,OA水平,CD是一段水平光滑轨道.一根长为2R、粗细均匀的细棒,开始时正好搁在圆弧轨道两个端点上,现由静止释放细棒,则此棒最后在水平轨道上滑行的速度为__________.
圆弧形轨道,圆弧半径为R,O为圆心,OA水平,CD是一段水平光滑轨道.一根长为2R、粗细均匀的细棒,开始时正好搁在圆弧轨道两个端点上,现由静止释放细棒,则此棒最后在水平轨道上滑行的速度为__________.
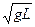 ?
?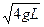 ?
?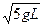
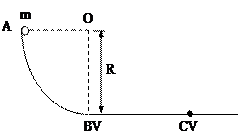
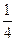 圆弧,AC的竖直高度差h=0.45m。在紧靠管道出口D处有一水平放置且绕其水平中心轴
圆弧,AC的竖直高度差h=0.45m。在紧靠管道出口D处有一水平放置且绕其水平中心轴 匀速旋转的圆筒,圆筒直径d=0.15m,桶上开有小孔E。现有质量为m=0.1kg且可视为质点的小球由静止开始从管口A滑下,小球滑到管道出口D处时,恰好能从小孔E竖直进入圆筒,随后,小球由小孔E处竖直向上穿出圆筒。不计空气阻力,取
匀速旋转的圆筒,圆筒直径d=0.15m,桶上开有小孔E。现有质量为m=0.1kg且可视为质点的小球由静止开始从管口A滑下,小球滑到管道出口D处时,恰好能从小孔E竖直进入圆筒,随后,小球由小孔E处竖直向上穿出圆筒。不计空气阻力,取 。求:
。求: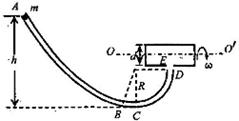
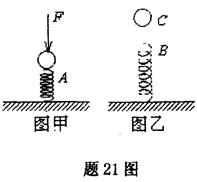
 下压至A静止,如图甲所示.然后突然撤去压力F,小球在竖直向上的运动过程中经过弹簧原长位置B最高能至C点,如图乙所示.不计空气阻力,重力加速度为g.下列说法正确的是:
下压至A静止,如图甲所示.然后突然撤去压力F,小球在竖直向上的运动过程中经过弹簧原长位置B最高能至C点,如图乙所示.不计空气阻力,重力加速度为g.下列说法正确的是: