题目内容
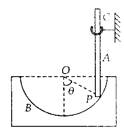
一个光滑的圆柱体固定在桌面上,圆柱体的半径为r。质量分别为mA和mB的两个小球A和B(都可看作质点,且mA>mB)用一根细线相连接,细线的长度恰好等于圆柱体的半个圆周长。开始时使两小球位于同一水平面上,如图所示,无初速地释放,求
①当A球到达桌面时,B球的速度多大?
②设A球落到桌面后即停止运动,求两球质量满足怎样的关系,小球B能滑过圆柱体的最高点并且继续沿圆柱体滑动一段?
①
 ;②
;②
①当A下落到达桌面时,B沿圆弧上升转过1rad,它上升的高度h=rsin1,如图所示。
设A球到达地面时两球的速率为v,根据机械能守恒定律,有mA gr- mB gh=
 ,
,h=rsin1。
解出v=
 。
。②A球到达桌面后,细线即松驰,B球由于惯性和重力作用将继续沿圆柱体向上运动,运动过程中B球的机械能守恒。设它经过最高点时的速度为v’,有
mBgr(1-sin1)=
 ,
,它能通过圆柱体的最高点并继续在圆周上运动一段的条件是
 ,
,解以上各式,可得
 。
。
练习册系列答案
相关题目
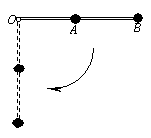
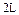 的轻杆上端及其正中央固定两个质量均为m的小球,杆的下端有光滑铰链与水平面相连接,杆原来竖直静止,现让其自由倒下,则A着地时的速度为( )
的轻杆上端及其正中央固定两个质量均为m的小球,杆的下端有光滑铰链与水平面相连接,杆原来竖直静止,现让其自由倒下,则A着地时的速度为( ) 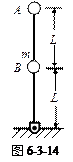
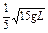
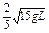
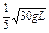
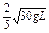
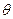

 ,BC面高出水面的距离
,BC面高出水面的距离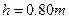 。一质量m=50kg的游戏者从滑梯顶端A点由静止滑下,
。一质量m=50kg的游戏者从滑梯顶端A点由静止滑下, 取10mol/s2。
取10mol/s2。 梯顶端A点由静止滑下到达滑梯末端C点时的速度大小
梯顶端A点由静止滑下到达滑梯末端C点时的速度大小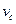 =15m/s,求这一过程中游戏者克服阻力做的功;
=15m/s,求这一过程中游戏者克服阻力做的功;