题目内容
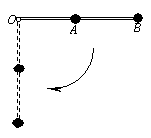
质量相同的两个小球,分别用长l和2l的细绳悬挂在天花板上,分别拉起小球,使细绳伸直呈水平状态后轻轻释放,当小球到达最低位置时( )
| A.它们的线速度相等 | B.它们的角速度相等 |
| C.它们的向心加速度相等 | D.绳对球的拉力相等 |
CD
物体从悬线水平释放后到最低点,由机械能守恒定律得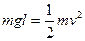 .
.
所以,小球到达最低点时的速度为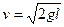
v与l有关,线越长,球到达最低点时的速度越大,A选项错.在最低点的角速度为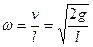 ,
,
ω与l有关,线越长,球到达最低点时的角速度越小,B选项错.球在最低点时的向心加速度为 ,a与l无关,两球的向心加速度相等,C选项正确.由牛顿第二定律得
,a与l无关,两球的向心加速度相等,C选项正确.由牛顿第二定律得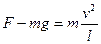 球在最低点时绳对球的拉力为F=3mg
球在最低点时绳对球的拉力为F=3mg
F与l无关,球到达最低点时,绳对球的拉力相等,
D选项正确.
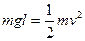 .
.所以,小球到达最低点时的速度为
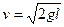
v与l有关,线越长,球到达最低点时的速度越大,A选项错.在最低点的角速度为
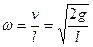 ,
,ω与l有关,线越长,球到达最低点时的角速度越小,B选项错.球在最低点时的向心加速度为
 ,a与l无关,两球的向心加速度相等,C选项正确.由牛顿第二定律得
,a与l无关,两球的向心加速度相等,C选项正确.由牛顿第二定律得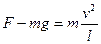 球在最低点时绳对球的拉力为F=3mg
球在最低点时绳对球的拉力为F=3mgF与l无关,球到达最低点时,绳对球的拉力相等,
D选项正确.

练习册系列答案
相关题目
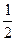 mv2时,对纸带上起点的要求是____________,为此目的,所选择的纸带一、二两点间距应接近_______________.
mv2时,对纸带上起点的要求是____________,为此目的,所选择的纸带一、二两点间距应接近_______________.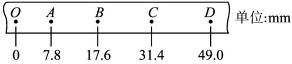
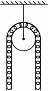
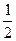 mv02?
mv02?