题目内容
8. 如图所示,让摆球从图中的A位置由静止开始摆动,正好到最低点B时线被拉断,已知摆线长L=1.6m,悬点距地面的竖直高度为H=6.6m,不计空气阻力(g取10m/s2),则摆球落地时的速度v=10.77m/s;落地点D到悬点O的正下方C点的水平距离为$2\sqrt{2}$m.
如图所示,让摆球从图中的A位置由静止开始摆动,正好到最低点B时线被拉断,已知摆线长L=1.6m,悬点距地面的竖直高度为H=6.6m,不计空气阻力(g取10m/s2),则摆球落地时的速度v=10.77m/s;落地点D到悬点O的正下方C点的水平距离为$2\sqrt{2}$m.
分析 小球从A到C的整个运动过程中,只有重力做功,机械能守恒,根据机械能守恒定律列式即可求解摆球落地时的速度.
先由机械能守恒定律求出小球到达B点的速度,小球从B点开始做平抛运动,由平抛运动的规律求解落地点D到C点的距离.
解答 解:整个的过程中只有重力做功,则:$\frac{1}{2}m{v}^{2}=mg(H-Lcos60°)$
代入数据得:v=10.77m/s
小球刚摆到B点时,由机械能守恒得:
mgL(1-cos60°)=$\frac{1}{2}m{v}_{B}^{2}$
代入数据可解得:vB=2$\sqrt{2}$m/s
小球离过B后,作平抛运动,竖直方向;H-L=$\frac{1}{2}g{t}^{2}$
解得:t=1s,
落地点D到C的距离
S=vBt
可解得:s=$2\sqrt{2}$m
故答案案为:10.77;$2\sqrt{2}$
点评 本题主要要掌握机械能守恒定律和平抛运动研究的方法:运动的分解法,选取好研究过程即可进行解题.

练习册系列答案
相关题目
19.如图甲所示,质量为m=11kg的木块静止在水平面上,现用与水平面成θ=37°角的力F拉着木块运动,5s后撤去拉力,木块运动的v-t图象如图乙所示,不计空气阻力,sin37°=0.6,cos37°=0.8,g=10m/s2,则下列说法正确的是( )
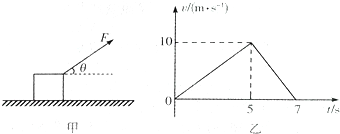

| A. | 木块与水平面间的动摩擦因数0.25 | |
| B. | 拉力F的大小为70N | |
| C. | 在0~7s内,木块克服摩擦力做功为1400J | |
| D. | 在2s时,拉力F的瞬时功率为280W |
16.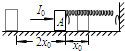 如图所示,劲度系数为k的轻弹簧的一端固定在墙上,另一端与置于水平面上质量为m的物体A接触,但未与物体A连接,弹簧水平且无形变.现对物体A施加一个水平向右的瞬间冲量,大小为I0,测得物体A向右运动的最大距离为x0,之后物体A被弹簧弹回最终停在距离初始位置左侧2x0处.已知弹簧始终在弹簧弹性限度内,物体A与水平面间的动摩擦因数为μ,重力加速度为g,下列说法中正确的是( )
如图所示,劲度系数为k的轻弹簧的一端固定在墙上,另一端与置于水平面上质量为m的物体A接触,但未与物体A连接,弹簧水平且无形变.现对物体A施加一个水平向右的瞬间冲量,大小为I0,测得物体A向右运动的最大距离为x0,之后物体A被弹簧弹回最终停在距离初始位置左侧2x0处.已知弹簧始终在弹簧弹性限度内,物体A与水平面间的动摩擦因数为μ,重力加速度为g,下列说法中正确的是( )
 如图所示,劲度系数为k的轻弹簧的一端固定在墙上,另一端与置于水平面上质量为m的物体A接触,但未与物体A连接,弹簧水平且无形变.现对物体A施加一个水平向右的瞬间冲量,大小为I0,测得物体A向右运动的最大距离为x0,之后物体A被弹簧弹回最终停在距离初始位置左侧2x0处.已知弹簧始终在弹簧弹性限度内,物体A与水平面间的动摩擦因数为μ,重力加速度为g,下列说法中正确的是( )
如图所示,劲度系数为k的轻弹簧的一端固定在墙上,另一端与置于水平面上质量为m的物体A接触,但未与物体A连接,弹簧水平且无形变.现对物体A施加一个水平向右的瞬间冲量,大小为I0,测得物体A向右运动的最大距离为x0,之后物体A被弹簧弹回最终停在距离初始位置左侧2x0处.已知弹簧始终在弹簧弹性限度内,物体A与水平面间的动摩擦因数为μ,重力加速度为g,下列说法中正确的是( )| A. | 物体A整个运动过程,弹簧对物体A的冲量为零 | |
| B. | 物体A向右运动过程中与弹簧接触的时间一定等于物体A向左运动过程中与弹簧接触的时间 | |
| C. | 物体A向左运动的最大动能Ekm=$\frac{{{I}_{0}}^{2}}{2m}$-2μmgx0 | |
| D. | 物体A与弹簧作用的过程中,系统的最大弹性势能Ep=$\frac{{{I}_{0}}^{2}}{2m}$-μmgx0 |
13.一物体从距离地面H高处自由下落,当其重力势能等于动能的3倍时(以地面为零势能面),物体的速度为( )
| A. | $\frac{1}{2}$$\sqrt{2gH}$ | B. | $\sqrt{gH}$ | C. | $\sqrt{2gH}$ | D. | 2$\sqrt{gH}$ |
17. 如图所示,现有一端固定在地面上的两根长度相同竖直弹簧(K1>K2),两个质量相同的小球分别由两弹簧的正上方高为H处自由下落,落到轻弹簧上将弹簧压缩,小球落到弹簧上将弹簧压缩的过程中获得的最大弹性势能分别是E1和E2,在具有最大动能时刻的重力势能分别是EP1和EP2(以地面为重力势能的零势能),则( )
如图所示,现有一端固定在地面上的两根长度相同竖直弹簧(K1>K2),两个质量相同的小球分别由两弹簧的正上方高为H处自由下落,落到轻弹簧上将弹簧压缩,小球落到弹簧上将弹簧压缩的过程中获得的最大弹性势能分别是E1和E2,在具有最大动能时刻的重力势能分别是EP1和EP2(以地面为重力势能的零势能),则( )
 如图所示,现有一端固定在地面上的两根长度相同竖直弹簧(K1>K2),两个质量相同的小球分别由两弹簧的正上方高为H处自由下落,落到轻弹簧上将弹簧压缩,小球落到弹簧上将弹簧压缩的过程中获得的最大弹性势能分别是E1和E2,在具有最大动能时刻的重力势能分别是EP1和EP2(以地面为重力势能的零势能),则( )
如图所示,现有一端固定在地面上的两根长度相同竖直弹簧(K1>K2),两个质量相同的小球分别由两弹簧的正上方高为H处自由下落,落到轻弹簧上将弹簧压缩,小球落到弹簧上将弹簧压缩的过程中获得的最大弹性势能分别是E1和E2,在具有最大动能时刻的重力势能分别是EP1和EP2(以地面为重力势能的零势能),则( )| A. | E1<E2 | B. | E1>E2 | C. | EP1=EP2 | D. | EP1>EP2 |
18.关于电势和电势能下列说法正确的是( )
| A. | 电荷在高电势的地方具有的电势能大 | |
| B. | 在电场中某一点,电荷的电量越大电势能就越大 | |
| C. | 正点电荷形成的电场中,正检验电荷的电势能一定大于负检验电荷的 | |
| D. | 电荷在等势面上移动时,电场力一定不做功 |
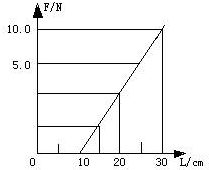 某同学在做“研究弹簧的形变与外力的关系”实验时,将一轻弹簧竖直(水平、竖直)悬挂让其自然下垂;然后在其下部施加外力F,测出弹簧的总长度L,改变外力F的大小,测出几组数据,作出外力F与弹簧总长度L的关系图线如图所示.(实验过程是在弹簧的弹性限度内进行的)由图可知该弹簧的自然长度为10cm;该弹簧的劲度系数为50N/m.
某同学在做“研究弹簧的形变与外力的关系”实验时,将一轻弹簧竖直(水平、竖直)悬挂让其自然下垂;然后在其下部施加外力F,测出弹簧的总长度L,改变外力F的大小,测出几组数据,作出外力F与弹簧总长度L的关系图线如图所示.(实验过程是在弹簧的弹性限度内进行的)由图可知该弹簧的自然长度为10cm;该弹簧的劲度系数为50N/m.
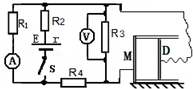 如图所示,水平放置的气缸内封闭了一定质量的理想气体,气缸的侧壁为光滑绝缘体,缸底M及活塞D均为导体并用导线按图连接,活塞面积S=2cm2.电键断开时,DM间距l1=5μm,闭合电键后,活塞D与缸底M分别带有等量异种电荷,并各自产生匀强电场(D与M间的电场为各自产生的电场的叠加).在电场力作用下活塞D发生移动,稳定后,DM间距l2=4μm,此时电流表读数为0.75A,电压表读数为2V,已知R4=4Ω,大气压强ρ0=1.0×105Pa,活塞移动前后气体温度不变.
如图所示,水平放置的气缸内封闭了一定质量的理想气体,气缸的侧壁为光滑绝缘体,缸底M及活塞D均为导体并用导线按图连接,活塞面积S=2cm2.电键断开时,DM间距l1=5μm,闭合电键后,活塞D与缸底M分别带有等量异种电荷,并各自产生匀强电场(D与M间的电场为各自产生的电场的叠加).在电场力作用下活塞D发生移动,稳定后,DM间距l2=4μm,此时电流表读数为0.75A,电压表读数为2V,已知R4=4Ω,大气压强ρ0=1.0×105Pa,活塞移动前后气体温度不变.