题目内容
16.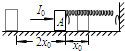 如图所示,劲度系数为k的轻弹簧的一端固定在墙上,另一端与置于水平面上质量为m的物体A接触,但未与物体A连接,弹簧水平且无形变.现对物体A施加一个水平向右的瞬间冲量,大小为I0,测得物体A向右运动的最大距离为x0,之后物体A被弹簧弹回最终停在距离初始位置左侧2x0处.已知弹簧始终在弹簧弹性限度内,物体A与水平面间的动摩擦因数为μ,重力加速度为g,下列说法中正确的是( )
如图所示,劲度系数为k的轻弹簧的一端固定在墙上,另一端与置于水平面上质量为m的物体A接触,但未与物体A连接,弹簧水平且无形变.现对物体A施加一个水平向右的瞬间冲量,大小为I0,测得物体A向右运动的最大距离为x0,之后物体A被弹簧弹回最终停在距离初始位置左侧2x0处.已知弹簧始终在弹簧弹性限度内,物体A与水平面间的动摩擦因数为μ,重力加速度为g,下列说法中正确的是( )| A. | 物体A整个运动过程,弹簧对物体A的冲量为零 | |
| B. | 物体A向右运动过程中与弹簧接触的时间一定等于物体A向左运动过程中与弹簧接触的时间 | |
| C. | 物体A向左运动的最大动能Ekm=$\frac{{{I}_{0}}^{2}}{2m}$-2μmgx0 | |
| D. | 物体A与弹簧作用的过程中,系统的最大弹性势能Ep=$\frac{{{I}_{0}}^{2}}{2m}$-μmgx0 |
分析 对物体的运动过程进行分析,由冲量的定义可明确弹力的冲量;根据运动过程分析以及牛顿第二定律可明确物体向左和向右运动过程中的加速度,则可明确对应的时间大小;物体在向左运动至弹力与摩擦力相等时速度达最大,根据功能关系可求得物体的最大动能以及最大弹性势能.
解答 解:A、由于弹簧的弹力一直向左,根据冲量的定义I=Ft,知弹力的冲量不可能为零,故A错误;
B、物体向右运动过程受向左的弹力和摩擦力,而向左运动过程中受向左的弹力与向右的摩擦力,因此向左运动时的加速度小于向右运动时的加速度;而与弹簧接触向左和向右的位移大小相等,则由位移公式可得,向右运动的时间一定小于向左运动的时间;故B错误;
C、物体在向左运动至弹力与摩擦力相等时速度达最大,动能最大,设物体的最大动能为Ekm.此时的压缩量为x,弹簧的弹性势能为EP.
从动能最大位置到最左端的过程,由功能关系有:Ekm+EP=μmg•(x+2x0)
从开始到向左动能最大的过程,有 $\frac{{{I}_{0}}^{2}}{2m}$=Ekm+EP+μmg•(2x0-x),联立解得 Ekm=$\frac{{{I}_{0}}^{2}}{2m}$-2μmgx>$\frac{{{I}_{0}}^{2}}{2m}$-2μmgx0,故C错误;
D、由动量定理可知I0=mv0,由功能关系知,系统具有的最大弹性势能 EP=$\frac{1}{2}$mv02-μmgx0=$\frac{{{I}_{0}}^{2}}{2m}$-μmgx0;故D正确;
故选:D
点评 本题为力学综合性题目,要求学生能正确分析问题,根据题意明确所对应的物理规律的应用,运用功能关系、牛顿第二定律及运动学公式分析.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
6.甲、乙两小球都在水平面上做匀速圆周运动,它们的线速度大小之比为1:2,角速度大小之比为3:1,则两球的向心加速度大小之比为( )
| A. | 1:2 | B. | 2:1 | C. | 2:3 | D. | 3:2 |
7.理想气体微观模型基本假设是( )
| A. | 只考虑气体分子间的引力作用 | |
| B. | 只考虑气体分子间的斥力作用 | |
| C. | 既考虑气体分子间的引力又考虑斥力作用 | |
| D. | 把气体分子看作没有大小的刚性球 |
4. 如图所示,木块静止在光滑水平桌面上,一子弹水平射入木块的深度为d时,子弹与木块相对静止,在子弹入射的过程中,木块沿桌面移动的距离为L,木块对子弹的平均阻力为f,那么在这一过程中正确的是( )
如图所示,木块静止在光滑水平桌面上,一子弹水平射入木块的深度为d时,子弹与木块相对静止,在子弹入射的过程中,木块沿桌面移动的距离为L,木块对子弹的平均阻力为f,那么在这一过程中正确的是( )
 如图所示,木块静止在光滑水平桌面上,一子弹水平射入木块的深度为d时,子弹与木块相对静止,在子弹入射的过程中,木块沿桌面移动的距离为L,木块对子弹的平均阻力为f,那么在这一过程中正确的是( )
如图所示,木块静止在光滑水平桌面上,一子弹水平射入木块的深度为d时,子弹与木块相对静止,在子弹入射的过程中,木块沿桌面移动的距离为L,木块对子弹的平均阻力为f,那么在这一过程中正确的是( )| A. | 木块的机械能增量为fL | B. | 子弹的机械能减少量为fL | ||
| C. | 系统的机械能减少量为f(L+d) | D. | 以上说法均错 |
11. 把质量为m的小球放在竖直的轻质弹簧上,并把球往下按至A的位置,如图甲所示.迅速松手后,弹簧把球弹起,球升至最高位置C点(图丙),途中经过位置B时弹簧处于自由状态(图乙).已知B、A的高度差为h1,C、A的高度差为h2,重力加速度为g,则( )
把质量为m的小球放在竖直的轻质弹簧上,并把球往下按至A的位置,如图甲所示.迅速松手后,弹簧把球弹起,球升至最高位置C点(图丙),途中经过位置B时弹簧处于自由状态(图乙).已知B、A的高度差为h1,C、A的高度差为h2,重力加速度为g,则( )
 把质量为m的小球放在竖直的轻质弹簧上,并把球往下按至A的位置,如图甲所示.迅速松手后,弹簧把球弹起,球升至最高位置C点(图丙),途中经过位置B时弹簧处于自由状态(图乙).已知B、A的高度差为h1,C、A的高度差为h2,重力加速度为g,则( )
把质量为m的小球放在竖直的轻质弹簧上,并把球往下按至A的位置,如图甲所示.迅速松手后,弹簧把球弹起,球升至最高位置C点(图丙),途中经过位置B时弹簧处于自由状态(图乙).已知B、A的高度差为h1,C、A的高度差为h2,重力加速度为g,则( )| A. | 状态甲中弹簧的弹性势能为mgh2 | |
| B. | 小球由状态甲到状态乙的过程中速度一直增大 | |
| C. | 小球由状态甲到状态乙的过程中机械能守恒 | |
| D. | 状态乙中小球的动能最大 |
1.下列实例中,机械能守恒的是( )
| A. | 物体沿光滑曲面滑下 | B. | 拉着一个物体沿光滑斜面匀速上升 | ||
| C. | 降落伞吊着重物在空气中匀速下落 | D. | 氢气球匀速上升 |
 如图所示,让摆球从图中的A位置由静止开始摆动,正好到最低点B时线被拉断,已知摆线长L=1.6m,悬点距地面的竖直高度为H=6.6m,不计空气阻力(g取10m/s2),则摆球落地时的速度v=10.77m/s;落地点D到悬点O的正下方C点的水平距离为$2\sqrt{2}$m.
如图所示,让摆球从图中的A位置由静止开始摆动,正好到最低点B时线被拉断,已知摆线长L=1.6m,悬点距地面的竖直高度为H=6.6m,不计空气阻力(g取10m/s2),则摆球落地时的速度v=10.77m/s;落地点D到悬点O的正下方C点的水平距离为$2\sqrt{2}$m. 如图所示,平行于光滑斜面的轻弹簧劲度系数为k,一端固定在倾角为θ的斜面底端,另一端与物块A连接,物块B沿斜面叠放在物块A上但不黏连.光滑斜面轨道与传送轨道良好对接,传送轨道平面与水平方向倾角也是θ,皮带传动装置顺时针匀速转动,物块A,B质量均为m,初始时两物块均静止.现用平行于斜面向上的拉力拉动物块B,使B做加速度为a的匀加速运动,两物块在开始一段时间内的v-t图象如图所示(t1时刻A、B的图线相切,t2时刻对应A图线的最高点),重力加速度为g,(t1和t2,v1和v2均未知)
如图所示,平行于光滑斜面的轻弹簧劲度系数为k,一端固定在倾角为θ的斜面底端,另一端与物块A连接,物块B沿斜面叠放在物块A上但不黏连.光滑斜面轨道与传送轨道良好对接,传送轨道平面与水平方向倾角也是θ,皮带传动装置顺时针匀速转动,物块A,B质量均为m,初始时两物块均静止.现用平行于斜面向上的拉力拉动物块B,使B做加速度为a的匀加速运动,两物块在开始一段时间内的v-t图象如图所示(t1时刻A、B的图线相切,t2时刻对应A图线的最高点),重力加速度为g,(t1和t2,v1和v2均未知) 如图所示,物体A的质量为2m,物体B的质量为m,A与地面的动摩擦因数为μ,B与地面的摩擦不计,用水平力F向右推A使A、B一起加速运动,求:
如图所示,物体A的质量为2m,物体B的质量为m,A与地面的动摩擦因数为μ,B与地面的摩擦不计,用水平力F向右推A使A、B一起加速运动,求: