题目内容
17. 如图所示,现有一端固定在地面上的两根长度相同竖直弹簧(K1>K2),两个质量相同的小球分别由两弹簧的正上方高为H处自由下落,落到轻弹簧上将弹簧压缩,小球落到弹簧上将弹簧压缩的过程中获得的最大弹性势能分别是E1和E2,在具有最大动能时刻的重力势能分别是EP1和EP2(以地面为重力势能的零势能),则( )
如图所示,现有一端固定在地面上的两根长度相同竖直弹簧(K1>K2),两个质量相同的小球分别由两弹簧的正上方高为H处自由下落,落到轻弹簧上将弹簧压缩,小球落到弹簧上将弹簧压缩的过程中获得的最大弹性势能分别是E1和E2,在具有最大动能时刻的重力势能分别是EP1和EP2(以地面为重力势能的零势能),则( )| A. | E1<E2 | B. | E1>E2 | C. | EP1=EP2 | D. | EP1>EP2 |
分析 小球压缩弹簧的过程中,受重力和弹力,在平衡位置,动能最大;结合动能定理和能量守恒定律分析即可.
解答 解:小球压缩弹簧的过程中,受重力和支持力,在平衡位置,速度最大,动能最大,根据平衡条件,有:
kx=mg
解得:x=$\frac{mg}{k}$
由于K1>K2,所以K1弹簧的弹力先等于重力,小球的动能最大时即K1弹簧的压缩量小,小球的位置高,可知在具有最大动能时刻的重力势能分别是EP1>EP2.
由于K1>K2,弹簧K1先更难被压缩,所以到达最低点时,弹簧K1的压缩量小,小球的位置比较高,则小球减小的重力势能比较小,根据小球与弹簧的系统的机械能守恒可知,弹簧K1的弹性势能就比较小E1<E2;所以选项AD正确,BC错误.
故选:AD
点评 本题关键明确小球压缩弹簧的过程中,弹簧和小球系统机械能守恒,在平衡位置速度最大,基础问题.

练习册系列答案
相关题目
7.理想气体微观模型基本假设是( )
| A. | 只考虑气体分子间的引力作用 | |
| B. | 只考虑气体分子间的斥力作用 | |
| C. | 既考虑气体分子间的引力又考虑斥力作用 | |
| D. | 把气体分子看作没有大小的刚性球 |
12.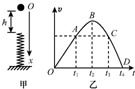 蹦床运动可简化为一个小球落到竖直放置轻弹簧上的运动,如图甲所示.质量为m的小球,从离弹簧上端高h处自由下落,接触弹簧后继续向下运动.以小球刚开始下落计时,以竖直向下为正方向,小球的速度v随时间t变化的图线如图乙所示.图线中的OA段为直线,与曲线ABCD相切于A点.不考虑空气阻力,则关于小球的运动过程,下列说法中正确的是( )
蹦床运动可简化为一个小球落到竖直放置轻弹簧上的运动,如图甲所示.质量为m的小球,从离弹簧上端高h处自由下落,接触弹簧后继续向下运动.以小球刚开始下落计时,以竖直向下为正方向,小球的速度v随时间t变化的图线如图乙所示.图线中的OA段为直线,与曲线ABCD相切于A点.不考虑空气阻力,则关于小球的运动过程,下列说法中正确的是( )
 蹦床运动可简化为一个小球落到竖直放置轻弹簧上的运动,如图甲所示.质量为m的小球,从离弹簧上端高h处自由下落,接触弹簧后继续向下运动.以小球刚开始下落计时,以竖直向下为正方向,小球的速度v随时间t变化的图线如图乙所示.图线中的OA段为直线,与曲线ABCD相切于A点.不考虑空气阻力,则关于小球的运动过程,下列说法中正确的是( )
蹦床运动可简化为一个小球落到竖直放置轻弹簧上的运动,如图甲所示.质量为m的小球,从离弹簧上端高h处自由下落,接触弹簧后继续向下运动.以小球刚开始下落计时,以竖直向下为正方向,小球的速度v随时间t变化的图线如图乙所示.图线中的OA段为直线,与曲线ABCD相切于A点.不考虑空气阻力,则关于小球的运动过程,下列说法中正确的是( )| A. | 下落h高度时小球速度最大 | |
| B. | 小球在t4时刻所受弹簧弹力大于2mg | |
| C. | t2-t1>t3-t2 | |
| D. | 球在t1到t4的时间内重力势能减小量大于弹簧弹性势能的增加量 |
 如图所示,让摆球从图中的A位置由静止开始摆动,正好到最低点B时线被拉断,已知摆线长L=1.6m,悬点距地面的竖直高度为H=6.6m,不计空气阻力(g取10m/s2),则摆球落地时的速度v=10.77m/s;落地点D到悬点O的正下方C点的水平距离为$2\sqrt{2}$m.
如图所示,让摆球从图中的A位置由静止开始摆动,正好到最低点B时线被拉断,已知摆线长L=1.6m,悬点距地面的竖直高度为H=6.6m,不计空气阻力(g取10m/s2),则摆球落地时的速度v=10.77m/s;落地点D到悬点O的正下方C点的水平距离为$2\sqrt{2}$m. 如图所示,平行于光滑斜面的轻弹簧劲度系数为k,一端固定在倾角为θ的斜面底端,另一端与物块A连接,物块B沿斜面叠放在物块A上但不黏连.光滑斜面轨道与传送轨道良好对接,传送轨道平面与水平方向倾角也是θ,皮带传动装置顺时针匀速转动,物块A,B质量均为m,初始时两物块均静止.现用平行于斜面向上的拉力拉动物块B,使B做加速度为a的匀加速运动,两物块在开始一段时间内的v-t图象如图所示(t1时刻A、B的图线相切,t2时刻对应A图线的最高点),重力加速度为g,(t1和t2,v1和v2均未知)
如图所示,平行于光滑斜面的轻弹簧劲度系数为k,一端固定在倾角为θ的斜面底端,另一端与物块A连接,物块B沿斜面叠放在物块A上但不黏连.光滑斜面轨道与传送轨道良好对接,传送轨道平面与水平方向倾角也是θ,皮带传动装置顺时针匀速转动,物块A,B质量均为m,初始时两物块均静止.现用平行于斜面向上的拉力拉动物块B,使B做加速度为a的匀加速运动,两物块在开始一段时间内的v-t图象如图所示(t1时刻A、B的图线相切,t2时刻对应A图线的最高点),重力加速度为g,(t1和t2,v1和v2均未知)
 如图所示,物体A的质量为2m,物体B的质量为m,A与地面的动摩擦因数为μ,B与地面的摩擦不计,用水平力F向右推A使A、B一起加速运动,求:
如图所示,物体A的质量为2m,物体B的质量为m,A与地面的动摩擦因数为μ,B与地面的摩擦不计,用水平力F向右推A使A、B一起加速运动,求: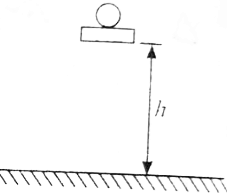 如图所示,弹性小球的质量为m,钢板的质量为M(M?m),它们一起自h高处自由下落,并与弹性地板相碰,不计空气阻力,球与钢板之间的碰撞及钢板与地面之间的碰撞均为弹性碰撞,试计算钢板着地后弹性小球能够上升高度.
如图所示,弹性小球的质量为m,钢板的质量为M(M?m),它们一起自h高处自由下落,并与弹性地板相碰,不计空气阻力,球与钢板之间的碰撞及钢板与地面之间的碰撞均为弹性碰撞,试计算钢板着地后弹性小球能够上升高度.