题目内容
19．如图甲所示，质量为m=11kg的木块静止在水平面上，现用与水平面成θ=37°角的力F拉着木块运动，5s后撤去拉力，木块运动的v-t图象如图乙所示，不计空气阻力，sin37°=0.6，cos37°=0.8，g=10m/s2，则下列说法正确的是（ ）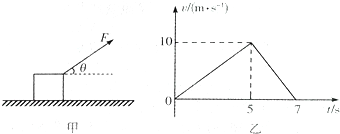
| A． | 木块与水平面间的动摩擦因数0.25 | |
| B． | 拉力F的大小为70N | |
| C． | 在0～7s内，木块克服摩擦力做功为1400J | |
| D． | 在2s时，拉力F的瞬时功率为280W |
分析 撤去拉力后木块做匀减速运动，由v-t图象的斜率求出加速度，再由牛顿第二定律求木块与水平面间的动摩擦因数．再研究有拉力作用的过程，由v-t图象求出加速度，再由牛顿第二定律求拉力F的大小．由位移公式求出0.7s内木块的位移，再由功的公式求克服摩擦力做功．由速度公式求出2s末木块的速度，再由公式P=Fvcosθ求瞬时功率．
解答 解：A、撤去拉力后木块做匀减速运动，由v-t图象的斜率可得，匀减速运动的加速度大小为 a2=$\frac{10}{7-5}$=5m/s2，由牛顿第二定律得：μmg=ma2，解得 μ=0.5，故A错误．
B、0-5s内木块的加速度为 a1=$\frac{v}{t}$=$\frac{10}{5}$=2m/s2，由牛顿第二定律得：Fcosθ-μ（mg-Fsinθ）=ma1，解得 F=70N，故B正确．
C、在0-7s内，木块的位移为 x=$\frac{1}{2}{a}_{1}{t}^{2}$=$\frac{1}{2}$×2×72=49m，木块克服摩擦力做功 W=μ（mg-Fsinθ）x=0.5×（11×10-70×0.6）×49=1666J，故C错误．
D、在2s时，木块的速度为 v=a1t=4m/s，此时拉力F的瞬时功率为 P=Fvcosθ=70×4×0.8W=224W，故D错误．
故选：B
点评 本题是牛顿第二定律和运动学公式结合处理动力学问题，加速度是关键量，是联系力和运动学关系的桥梁，在这种方法中是必求的量．
练习册系列答案
相关题目
9．下列关于多普勒效应的说法不正确的是（ ）
| A． | 彩超测血流速度是利用超声波的多普勒效应 | |
| B． | 交警经常利用超声波的多普勒效应测量行进中车辆的速度，来判断车辆是否超速 | |
| C． | 雷达定位是利用电磁波的多普勒效应 | |
| D． | 多普勒效应是指波源与观察者互相靠近或远离时，接收到波的频率发生了变化的现象 |
7．理想气体微观模型基本假设是（ ）
| A． | 只考虑气体分子间的引力作用 | |
| B． | 只考虑气体分子间的斥力作用 | |
| C． | 既考虑气体分子间的引力又考虑斥力作用 | |
| D． | 把气体分子看作没有大小的刚性球 |
4．
如图所示，木块静止在光滑水平桌面上，一子弹水平射入木块的深度为d时，子弹与木块相对静止，在子弹入射的过程中，木块沿桌面移动的距离为L，木块对子弹的平均阻力为f，那么在这一过程中正确的是（ ）
如图所示，木块静止在光滑水平桌面上，一子弹水平射入木块的深度为d时，子弹与木块相对静止，在子弹入射的过程中，木块沿桌面移动的距离为L，木块对子弹的平均阻力为f，那么在这一过程中正确的是（ ）| A． | 木块的机械能增量为fL | B． | 子弹的机械能减少量为fL | ||
| C． | 系统的机械能减少量为f（L+d） | D． | 以上说法均错 |
11．
把质量为m的小球放在竖直的轻质弹簧上，并把球往下按至A的位置，如图甲所示．迅速松手后，弹簧把球弹起，球升至最高位置C点（图丙），途中经过位置B时弹簧处于自由状态（图乙）．已知B、A的高度差为h1，C、A的高度差为h2，重力加速度为g，则（ ）
把质量为m的小球放在竖直的轻质弹簧上，并把球往下按至A的位置，如图甲所示．迅速松手后，弹簧把球弹起，球升至最高位置C点（图丙），途中经过位置B时弹簧处于自由状态（图乙）．已知B、A的高度差为h1，C、A的高度差为h2，重力加速度为g，则（ ）| A． | 状态甲中弹簧的弹性势能为mgh2 | |
| B． | 小球由状态甲到状态乙的过程中速度一直增大 | |
| C． | 小球由状态甲到状态乙的过程中机械能守恒 | |
| D． | 状态乙中小球的动能最大 |
如图所示，让摆球从图中的A位置由静止开始摆动，正好到最低点B时线被拉断，已知摆线长L=1.6m，悬点距地面的竖直高度为H=6.6m，不计空气阻力（g取10m/s2），则摆球落地时的速度v=10.77m/s；落地点D到悬点O的正下方C点的水平距离为$2\sqrt{2}$m．